1

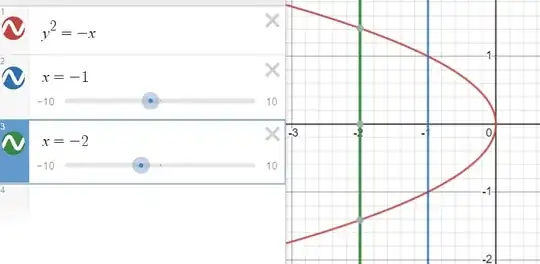
In high school textbooks, we see that while taking square roots, the negative sign is not taken in calculus problems. For example, when asked to find the area bounded by $y^2=-x$ between $-2$ to $-1,$ we do it like this: $$\int_{-2}^{-1} \sqrt{-x} \,\mathrm dx.$$ Why don't we take the $y=-\sqrt{-x}\,?$ In all calculus problems, why is it okay to only the take $\sqrt{a^2}=a$ instead of $\sqrt{a^2}=|a|\,?$

ryang
  • 38,879
  • 14
  • 81
  • 179
madness
  • 566
  • 1
    Which piece of area? From my understanding of the question, $y^2=-x$ becomes two curves $y=\sqrt{-x}$ and $y=-\sqrt{-x}$. Then to find the area between the two curves, I would calculate

    $$\int_{-2}^{-1}\left[\sqrt{-x} - (-\sqrt{-x})\right]dx$$

    (or multiply your integral result by $2$)

     – peterwhy Jun 10 '22 at 22:45
  • 1
    The standard definition of the symbol $\sqrt{}$ (for real numbers, at least) is that it is the positive root. This means $\sqrt{a^2} = |a|$ is always true, but $\sqrt{a^2} = a$ is not. – aschepler Jun 10 '22 at 22:49
  • @Dan actually i don't understand whether it answers my question,my doubt is if we have to take $y=\sqrt{-x}$ or $-\sqrt{-x}$ in such cases. – madness Jun 11 '22 at 04:57

2 Answers2

1

when asked to find the area bounded by $y^2=-x$ between $-2$ to $-1,$ we do it like this: $$\int_{-2}^{-1} \sqrt{-x} \,\mathrm dx.\tag1$$ Why don't we take the $y=-\sqrt{-x}\,?$

Perhaps you are showing just part of the working, since the required area in this example is obtained by multiplying expression $(1)$ by two, due to the figure's symmetry.

enter image description here

On the other hand, the signed area bounded by $y^2=-x$ between $-2$ to $-1$ does involve the $y=-\sqrt{-x}$ portion, and equals $$\int_{-2}^{-1} \sqrt{-x} \,\mathrm dx+\int_{-2}^{-1} -\sqrt{-x} \,\mathrm dx,$$ which equals $0.$

In all calculus problems, why is it okay to only the take $\sqrt{a^2}=a$ instead of $\sqrt{a^2}=|a|\,?$

This premise is false: the workings above are based on geometry rather than some generic calculus rule.

ryang
  • 38,879
  • 14
  • 81
  • 179
0

$y = -\sqrt{x}$ is complex on (-2,-1). you would get $y = -\sqrt{-1}$. What you want is $y=\sqrt{1}$. What you can do is let $z = -x$ then $dz = -dx$ and you get:

$$-\int_2^1 \sqrt{z} dz = \int_1^2 \sqrt{x} dx.$$

For your second question $\sqrt{(-1)^2} = \sqrt{1}=1 = |-1| \neq -1$.

Mark
  • 1,339