Solving $x^2-3-\operatorname{frac}(x)=0$

Question

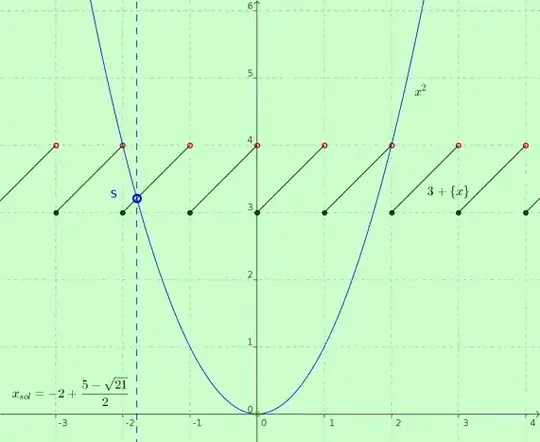
Problem. Solve the equation $$ x^2 - 3 - \operatorname{frac}(x) = 0 $$

I tried to solve this question by moving $3$ to the other side:

$$x^2 - \operatorname{frac}(x) = 3$$

Since the fractional part of R.H.S. is $0$,

$$ \operatorname{frac}\left(x^2\right) = \operatorname{frac}(x) \qquad\text{or}\qquad \operatorname{frac}\left(x^2\right) = 1 - \operatorname{frac}(x).$$

Since there is only 1 case for $\operatorname{frac}(x^2)=\operatorname{frac}(x)$ which is $\operatorname{frac}\left(x^2\right)=\operatorname{frac}(x)=0$ and no value of $x$ satisfies the equation, we can rule this condition out. We are left with $\operatorname{frac}\left(x^2\right)=1-\operatorname{frac}(x)$ and $x$ is negative, but I am stuck here.

Can anyone please give me an idea to proceed with this question?

Answer 1

Since $x^2 = 3 + \operatorname{frac}(x)$, we have $3 \leq x^2 < 4$. Solving this inequality, we have either

$$ \sqrt{3} \leq x < 2 \qquad\text{or} \qquad -2 < x \leq -\sqrt{3}. $$

• In the former case, we have $\lfloor x \rfloor = 1$ and hence we must have $$ x^2 = 3 + (x - 1) = x + 2. $$ However, solving this equation gives $x = -1$ or $x = 2$, none of which satisfying the restriction $\sqrt{3} \leq x < 2$. So, there is no solution of the equation in this case.

• In the latter case, we have $\lfloor x \rfloor = -2$, and so, we have $$ x^2 = 3 + (x + 2) = x + 5. $$ Solving this equation gives two values $x = \frac{1}{2}(1 \pm \sqrt{21})$, and indeed, the choice $$ x = \bbox[color:navy;padding:5px;border:1px navy dotted;]{\frac{1}{2}(1-\sqrt{21})} \approx -1.79129 $$ satisfies the equation.

Answer 2

Here's a start: Let $x = a + y$ where $a$ is an integer and $0\leq y <1$. Try a few values for $a$, such as $0, 1, 2, 3$ and then $-1, -2, -3$. I think you'll see how to proceed after that.

Answer 3

We have $$ 0 = x^2 - 3 - {\rm frac}(x) = x^2 - 3 - \left\{ x \right\} $$ where $$ x = \left\lfloor x \right\rfloor + \left\{ x \right\}\quad \left| {\,0 \le \left\{ x \right\} < 1} \right. $$

So we can put first of all $$ \eqalign{ & 3 \le x^2 = 3 + \left\{ x \right\} < 4\quad \Rightarrow \quad \sqrt 3 \le \pm x < 2\quad \Rightarrow \cr & \Rightarrow \quad \left( {\sqrt 3 \le x < 2} \right) \cup \left( { - 2 < x \le - \sqrt 3 } \right)\quad \Rightarrow \cr & \Rightarrow \quad \left( {1 \le \left\lfloor x \right\rfloor < 2} \right) \cup \left( { - 3 < \left\lfloor x \right\rfloor \le - 2} \right)\quad \Rightarrow \quad \left\lfloor x \right\rfloor = - 2,1 \cr} $$

Then, for $\left\lfloor x \right\rfloor = 1$ $$ \eqalign{ & 0 = x^2 - 3 - \left\{ x \right\} = \left( {1 + \left\{ x \right\}} \right)^2 - \left\{ x \right\} - 3 = \cr & = 1 + 2\left\{ x \right\} + \left\{ x \right\}^2 - \left\{ x \right\} - 3 = \cr & = \left\{ x \right\}^2 + \left\{ x \right\} - 2\quad \Rightarrow \cr & \Rightarrow \quad \left( {\left\{ x \right\} = - 2} \right) \cup \left( {\left\{ x \right\} = 1} \right) \quad \Rightarrow \cr & \Rightarrow \quad {\rm no}\;{\rm solution} \cr} $$ while for $\left\lfloor x \right\rfloor = -2$ $$ \eqalign{ & 0 = x^2 - 3 - \left\{ x \right\} = \left( { - 2 + \left\{ x \right\}} \right)^2 - \left\{ x \right\} - 3 = \cr & = 4 - 4\left\{ x \right\} + \left\{ x \right\}^2 - \left\{ x \right\} - 3 = \cr & = \left\{ x \right\}^2 - 5\left\{ x \right\} + 1\quad \Rightarrow \cr & \Rightarrow \quad \left( {\left\{ x \right\} = {{5 + \sqrt {21} } \over 2}} \right) \cup \left( {\left\{ x \right\} = {{5 - \sqrt {21} } \over 2}} \right)\quad \Rightarrow \cr & \Rightarrow \quad \left\{ x \right\} = {{5 - \sqrt {21} } \over 2} \cr} $$ That means that for $x$ we get $$ x = \left\lfloor x \right\rfloor + \left\{ x \right\} = - 2 + {{5 - \sqrt {21} } \over 2} = {{1 - \sqrt {21} } \over 2} $$ which is the same as the solution indicated by S. Lee

This is the graphical representation of the above