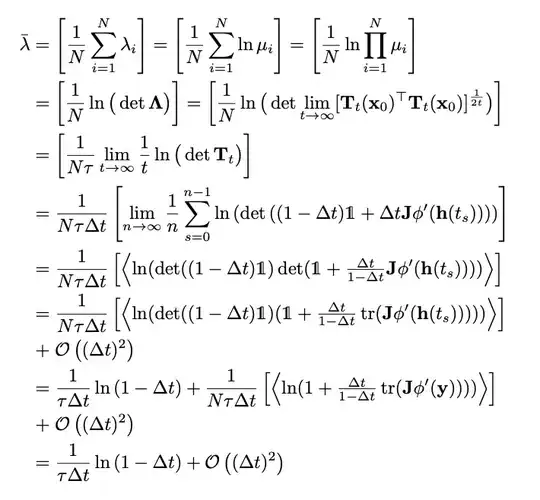$M$ is an iid random matrix with $M_{ij} \sim \mathcal{N}(0,\frac{g^2}N)$ except that the diagonal entries are $-1$.
I am to compute, in the limit $N\to\infty$,
the eigenvalue/singular value spectrum/distribution. I.e. we order the eigenvalues according to their relevant values such that $\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_N$, and then we hope to know the mean of each $\lambda_i$) of a random matrix $M$: $$\bar \lambda_1, \bar\lambda_2, \dots, \bar \lambda_N.$$
the mean ($\ln$) thereof: $$\langle \ln \lambda \rangle = \frac{\ln\lambda_1 + \ln\lambda_2 + \dots + \ln\lambda_N}N.$$
It seems we can calculate $\langle \ln \lambda \rangle$ using $\det(M)$. Then how can we compute the determinant (also a statistics) of such a random matrix?
We possibly need to use the Wigner semicircular law.
Possible methods in random matrices or more general probability include
reductions, the Fourier method, the moment method, the Lindeberg swapping trick, individual swapping, Stein's method, Predecessor comparison.
$\\$
I hope to know any books or papers about solving the above (or other) statistics of this (or simpler similar) random matrix, or of other 'symmetric' (w.r.t. probability distribution of each entry) matrices, or of other kinds of (large) square random matrices. The literature of random matrices is vast so I hope to narrow down the scope of my research. I can read them to find clues. Exact solutions are welcome but not necessarily expected right now.
This seems to be a seminal paper in the topic: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.60.1895
A closely related post: https://mathoverflow.net/questions/352559/spectrum-of-large-random-asymmetric-matrices-with-correlation
This is a simple example: Determinant of a random matrix, but it doesn't tell much about the statistics I would like to compute.
Appendix 1.
My thoughts about q1: An idea might be to first calculate the probability density for the vector random variable: $\rho_N ( \lambda_1, \lambda_2, \dots, \lambda_N),$ but $N\to\infty$ might complicate the issue of defining such a density.
About q2: Perhaps since sum of ln = ln of product, and product of eigenvalues = determinant, the calculation might be thus simplified, as illustrated below.
Appendix 2.
(This section is unnecessary for answering the question:) An example of calculation is given as (note that $\mu_i$ below is actually eigenvalues (specifically, of an Oseledets matrix $\Lambda$) denoted as $\lambda_i$ above. I hope to know what is more general than the example):
For this example in particular, why $$\prod_i \mu_i = \det(\Lambda)?$$
My thought is that we can transform $\Lambda$ to a diagonal matrix $D$ with a unitary matrix $P$:
$\Lambda = P D P^{-1},$
where $D_{ii} = \mu_i$ (or the eigenvalues in different order), $\det(P) = \det(P^{-1})=1$, and so
$$\det (\Lambda) = \det(P) \det (D) \det(P^{-1})=\det (D) =\prod_i \mu_i.$$
(In a word, the reason for the above step is that the determinant of an $n\times n$ matrix is always equal to the product of its eigenvalues, if the matrix has complete set of eigenvalues, i.e. #eigenvalues = $n$. A related discussion is here: Show that the determinant of $A$ is equal to the product of its eigenvalues)
Is it correct? (No need to answer this question here.)