the universal covering space of compact Riemann surface(how the covering map be holormporphic?)

Question

I occured in this question when I was learning the proof of the Riemann-Roch theorem for effective divisors with the vedio here(Sorry for this vedio is in Chinese, though the blackboard is written in English).

Suppose we have a compact Riemann surface $M$, and $\eta$ a abelian differential of the second kind(all poles has Residue $0$), and $\widetilde{M}$ the universal covering space of $M$. I saw such an argument:

Since $\eta$ has no simple poles, its pullback $\pi^* \eta$ in $\widetilde{M}$ has no simple poles too. Again by $\widetilde{M}$ being simply connected. $\int^{z}_{z_0} \pi^* \eta$ defines a meromorphic function $f(z)$ on $\widetilde{M}$ such that $\textrm{d}f = \pi^* \eta$.

The question I has is that altough considering $M$ as a topological manifold, its universal covering map $\pi: \widetilde{M} \to M$ is continuous. But here I believe that $\widetilde{M}$ should be constructed such that it has a $2$-complex structure and the covering map $\pi$ should be a holomorphic map.

My Questions:

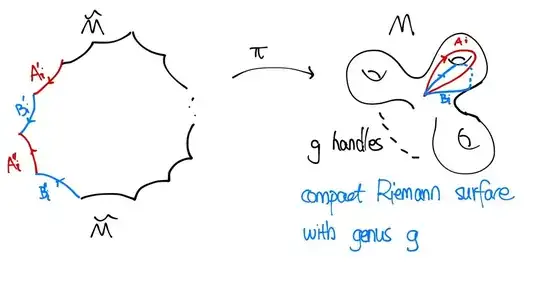
1. How to define the complex structure on $ \widetilde{M} $ such that the covering map $\pi$ is a holomorphic map? I think a way to define it is using the homotopy classs on $M$, but such a way does not give a $4g$-gon visualization.
2. If directly constructing $ \widetilde{M} $ via pasting many $4g$-gons, how to paste it together? for $g=2$ it's easy to imagine. But for $g > 2$ I cannot imagine it.
3. Does the proof for Riemann Roch theorem in the effective divisors case rely on the universal covering? In the vedio I watched, it has to pullback some form and integrating it in the boundary of the $4g$-gon to get the Period matrix.

Thanks!

Answer 1

I'm going to answer questions 1 and 2. Question 3 is rather different and is best handled in another post (we generally ask that you ask one question per post).

Start by applying the definitions of Riemann surfaces and of covering maps together, to choose an open covering $\{V_i\}$ of the Riemann surface $M$ which serves two purposes simultaneously:

• $\{V_i\}$ forms an atlas for the Riemann surface structure on $M$, so there is a "coordinate chart" homeomorphism $\phi_i : V_i \to W_i \subset \mathbb C$ such that $W_i$ is open and such that each overlap map is holomorphic.
• Each $V_i$ is an evenly covered open set with respect to the covering map $\pi : \widetilde M \to M$, so there is a disjoint union $\pi^{-1}(V_i) = \sqcup_j U_{ij}$ such that each $U_{ij} \subset \widetilde M$ is open and each restriction $\pi \mid U_{ij} : U_{ij} \to V_i$ is a homeomorphism.

Tracing through all of this it is pretty straightforward to prove that $\{U_{ij}\}$ forms an atlas for a Riemann surface structure on $\widetilde M$, using the "coordinate chart" homeomorphisms $$U_{ij} \xrightarrow{\pi \mid V_{ij}} V_{ij} \xrightarrow{\phi_i} W_i \subset \mathbb C $$ In fact, each overlap map of the atlas $\{U_{ij}\}$ of $\widetilde M$ is (the restriction of) one of the overlap maps of the atlas $U_i$ of $M$, and hence is holomorphic.

Finally, from this construction it should be pretty clear that the covering map $\pi : \widetilde M \to M$ is holomorphic: each restriction $U_{ij} \mapsto V_i$ is holomorphic because, when expressed in terms of the two coordinate charts $U_{ij} \to W_i$ and $V_i \to W_i$ the restriction is actually the identity map on $W_i$.