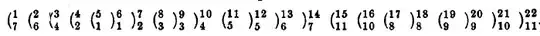Kleene: sets of parentheses and proper parentheses

Question

The following is from Introduction to Metamathematics by Steven Kleene. In Lemma 2 of section 7 of chapter 2, it seems ambiguous what constitutes a “set of parentheses.” Here are some relevant passages:

Proper pairing: a one-to-one pairing between n left parentheses "(" and n right parentheses ")" such that for each pair left parenthesis is on the left from the right parenthesis and if no two pairs separate each other.

Pairs of parentheses that separate each other - two pairs separate each other if they occur in the order (()).

Lemma 2 is as follows, in which I am uncertain as to the interpretation of “set of 2n parentheses…”

Lemma 2: A set of 2 parentheses admits at most one proper pairing.

What constitutes a pair of parentheses in a formula, and how are two distinct sets of parentheses distinguished? For instance, given the string “abc” are (a)bc and (abc) both a set of 2n parentheses (for n=1)? Otherwise, another scenario I can imagine is a pair of parenthesis being fixed in place in a formula, and the possibility of swapping the left and right mates is the only ‘degree of freedom’ in maintaining the “same set” criterion, but allowing for different strings of symbols.

Would anyone please illuminate this as it is meant to be intended?

To say a set of 2n parentheses means that there are an even number of them. — Mauro ALLEGRANZA, May 31 '22 at 17:43
The gist is: in a correctly written formula parenthese must be in an even number, in pairs and the pair must be () and not e.g. )( — Mauro ALLEGRANZA, May 31 '22 at 17:45
Examples: (((( even but not pairing, )()( even and pairing but not proper, (()) proper pairing. — Mauro ALLEGRANZA, May 31 '22 at 18:02
@MauroALLEGRANZA In that case, I could have a formula “(a or b) or c” (with one set) and a formula “a or (b or c)” (Also with one set), both being properly paired. — Cyrus, May 31 '22 at 18:12
Yes, in which case I’d have a set of parentheses for which there are two potential proper pairings, making the lemma seemingly false. — Cyrus, May 31 '22 at 19:54
Related: Proving by induction that a balanced strings of parentheses has equally many opening and closing parentheses (30 January 2016) AND this answer to Highly Rigorous Logic Book (1 November 2017) AND Kleene "Introduction to Metamathematics" problem on parentheses (10 July 2018) AND Error in Kleene "Introduction to Metamathematics" parentheses lemmas? (21 July 2020) — Dave L. Renfro, Jun 01 '22 at 10:09

Tankut Beygu · Answer 1 · 2022-06-01T11:01:46.123

Let us go over the section with examples of parenthetical structure of formulas (dots for readability):

We define a 1-1 pairing of the n left parentheses with the n right parentheses (briefly, a pairing of the 2n parentheses) to be proper, if a left parenthesis is always paired with a right parenthesis to the right of it, and if no two of the pairs separate each other.

$(_{k}.(_{}.(_{}.)_{}.)_{}.)_{k}$

i-pair separates j-pair, and vice versa; thus two pairs separate each other (improper pairing); therefore k-pair is not proper.

Lemma 1. A proper pairing of 2n parentheses (n > 0) contains an innermost pair, i.e. a pair which includes no other of the parentheses between them.

For n = 1, i.e., the lone pairs $(.)$, are vacuously innermost.

For n = 3, there is an innermost pair (bold-faced): $(.(.\mathbf{(.)}.).)$.

Lemma 2. A set of 2n parentheses admits at most one proper pairing.

Withdraw the innermost pair stated in Lemma 1 inductively:

$(.(.(.(.).).).)$

$(.(.(.).).)$

$(.(.).)$

$(.)$

Lemma 3. If 2n parentheses and a consecutive subset of 2m of them both admit proper pairings, then the proper pairing in the subset forms a part of the proper pairing in the whole set, i.e. each parenthesis of the subset has the same mate in both pairings.

Remark: "consecutive subset" is a subset of parentheses such that parentheses are placed consecutively.

Kleene's example:

$n = 22$ indicated by superscripts.

$m = 10$ from 3rd to 12th; pairing indicated by subscripts.

A consecutive set of properly paired parentheses, however it is placed in a larger set of parentheses, preserves the mates of each pair, unless consecution is spoiled.

Kleene: sets of parentheses and proper parentheses

1 Answers1