Why do different calculators disagree on $\cos(452175521116192774 )$?

Question

I want to calculate cosine of 452175521116192774 radians (it is around $4.52\cdot10^{17}$)
Here is what different calculators say:

Wolframalpha

Desmos

Geogebra

Python 3.9 (standard math module)

Python 3.9 (mpmath library)

Obviously there is only one solution. There could be errors in floating point precision for these calculators, but this stumbles me. My calculator (TI-30XIS) says domain error (which is weird because cosine of, for example, a billion works just fine). How can I get the cosine of very large integers?

Answer 1

The problem is that your integer $$n=452175521116192774$$ can't be stored exactly as a standard 64-bit IEEE double precision floating point number. The closest double happens to be $$x=452175521116192768,$$ as can be seen from the binary representation $$ \begin{aligned} n &= 11001000110011100110011110110100000010000100000000000\color{red}{000110}_2 \\ x &= 11001000110011100110011110110100000010000100000000000\color{red}{000000}_2 \end{aligned} $$ where those last few bits in $n$ are lost, since the double format only stores the first 52 digits after the leading “1”.

So in systems that use standard floating point (like Desmos, Geogebra, and the Python math module) you will actually get $x$ when you enter $n$ in a place where a double is expected; in Python you can verify this as follows:

> print("%.310g" % 452175521116192774)
452175521116192768

Conseqently, when you ask for $\cos n$ these systems will answer with $$\cos x = -0.2639 \ldots$$ (which in itself is computed correctly; it's just that the input is not what you thought).

In contrast, Wolfram Alpha and mpmath work with the exact number $n$, and give the correct answer $$\cos n = -0.5229 \ldots$$

Answer 2

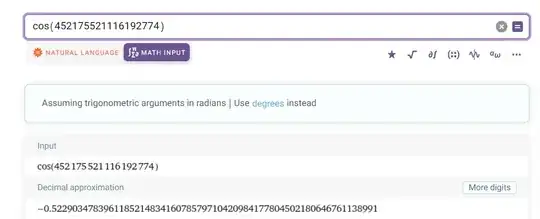
As Hans Lundmark pointed out, the problem is caused by converting the argument to a C double before doing the calculation.

But if you don't want to bring in a high-precision math library, there's a way (at least in Python) to calculate a more accurate value by using the sum-of-angles identities.

from math import cos, sin
def cossin(x):
    '''
    Return (cos(x), sin(x)) more accurately.
    '''
    if abs(x) < 2 ** 53:
        # All integers below this threshold are represented exactly,
        # so just use the normal math module functions.
        return (cos(x), sin(x))
    else:
        a = float(x)
        b = x - int(a)  # the approximation error
        # a is a float, so use the normal math functions.
        cos_a = cos(a)
        sin_a = sin(a)
        # for b, call recursively in case it can't be represented as float
        cos_b, sin_b = cossin(b)
        return (cos_a * cos_b - sin_a * sin_b, cos_a * sin_b + sin_a * cos_b)

This agrees pretty closely with WolframAlpha's result.

>>> cossin(452175521116192774)
(-0.5229034783961185, -0.8523919006426797)

---

An alternative approach is to use a high-precision approximation of π to reduce the argument modulo 2π. (In Python, you can use the Fraction class to store your approximation. This gives you:

$$452175521116192774 \approx 71965969330795778 \times 2\pi + 4.162135302888925$$

And taking the cosine of the reduced argument will give you the correct result.

>>> cos(4.162135302888925)
-0.5229034783961188

Answer 3

Your Texas Instruments calculator is probably an inferior model created by engineers did their best while under severe time and budget constraints, overseen by brutal capitalist managers who only care about meeting certain milestones in a Gantt chart.

My WP-34S (in double precision mode) is able to represent your number with a digit to spare. Pushing our luck, the cosine function in radian mode yields -0.52290347840 in the display. Alas, this calculator was too good, so HP discontinued the HP 30b Business Professional platform it was built on. But you can download a free emulator for your iPhone. That emulator runs long programs MUCH faster than the original calculator hardware.

How would YOU compute such a monster? Subtract an appropriate multiple of 2 pi to get the argument into a range the calculator can handle? Sorry, you don't have enough digits to do that.

I think your best bet would be to divide the argument by some large power of 2, then use the double angle formulas repeatedly to get the trig function of your desired angle. Alas, the largest power of 2 that divides your argument is 2. After that, further division by two adds more digits than your machine can hold. You need quad precision floating point to represent your argument in a computer, and much more than that to represent the argument divided by a large power of two. And if you can't even represent it, you can't calculate the cosine.