I am doing RSA questions and I really could use help! Can someone show me a simple way to find $25^9 \pmod{33}$?
-
you use long devision to find the remainder. For these types of numbers computer programs might be nice. – Thomas Rot Jun 10 '11 at 11:22
-
333 is not a large number. – Jan 01 '13 at 15:57
6 Answers
The standard way to compute $a^b\pmod m$ is to use repeated squaring and multiplying, reducing modulo $m$ at each step. In particular, $$25^9=(((25^2)^2)^2)(25)$$ so first you do $25^2=625$, then $625=33\times18+31$, $31^2=961$, $961=33\times29+4$, $4^2=16$, $16\times25=400$, $400=33\times12+4$, answer is $4$.
EDIT: More details can be found in the answers to an earlier question, calculating $a^b \!\mod c$
- 179,216
Using Euler's theorem,
$$a^{\phi(n)} \equiv 1 \mod n$$
for $a$ coprime to $n$, where $\phi(n)$ is the totient function.
Since $33=11\times 3$ you have $\phi(33) = \phi(11)\phi(3) = 10\times 2 = 20$, and therefore
$$25^9 = (5^2)^9 = 5^{18} = 5^{20} 5^{-2} \equiv 5^{-2} \mod 33$$
Now notice that $5\times 20 = 100$ which is one more than a multiple of $33$, so
$$5^{-1}\equiv 20 \mod 33$$
and hence
$$5^{-2} = 20^2 = 400 = 4\times 100 \equiv 4\times 1 = 4 \mod 33$$
- 28,955
-
Dear editor - not only did you screw up the math in this post by editing it, you also screwed up the formatting. I have reverted your edit. – Chris Taylor Feb 06 '15 at 22:39
You write
Mod[25^9, 33]
into Mathematica and the result is $4$.
Alternatively, if you don't have any computer, $25 = -8$ modulo $33$. So the result is just like $(-8)^9$ mod $33$. That's like $((-8)^3)^3$. Now, $(-8)^3$ is $-512$ modulo $33$ which is $-17$ because $512=33\times 15+17$. And $-17=+16$ modulo 33, and $16^3=4096 = 124\cdot 33+4$ which is $4$ modulo $33$.
- 8,078
For variety, let's invoke the Chinese remainder theorem
$$ 25^9 \equiv 1^9 \equiv 1 \pmod 3 $$ $$ 25^9 \equiv 3^9 \pmod{11}$$
That latter one isn't so bad to compute by repeated squaring:
$$ 3^9 \equiv 3 \cdot 3^8 \equiv 3 \cdot 9^4 \equiv 3 \cdot 81^2 \equiv 3 \cdot 4^2 \equiv 3 \cdot 5 \equiv 4 \pmod{11}$$
but I'm even lazier. Since $3^{10} \equiv 1 \pmod{11}$ (because $11$ is prime):
$$ 3^9 \equiv 3^{-1} \equiv 1/3 \equiv 12/3 \equiv 4 \pmod{11} $$
The extended Euclidean algorithm (or inspection) lets us compute
$$ 4 \cdot 3 + (-1) \cdot 11 = 1 $$
and therefore
$$ 25^9 \equiv 1 \cdot (-1 \cdot 11) + 4 \cdot (4 \cdot 3) \equiv -11 + 48 \equiv -11 + 15 \equiv 4 \pmod{33} $$
Ad-hoc: Carmichael $\rm\:\lambda(33) = lcm(\phi(3),\phi(11)) = 10\ \Rightarrow\ 25^9\equiv 1/25\equiv -1/8\equiv 4\ \ (mod\ 33)$
Algorthmic: use repeated squaring, which is easily recalled since it arises arises from writing the exponent in binary radix in Horner polynomial form, i.e. $\rm\ d_0 + x\ (d_1 + x\ (d_2\ +\:\cdots))\:.\ $ Below is an example of computing $\rm\ a^{101}\ $ by repeated squaring. Note that the repeated square form arises simply from performing various substitutions into the binary polynomial Horner form namely $\rm\ 1\to a,\ \ 0\to 1,\ \ (x)\:2\to (x)^2\ $ into $101_{10} = 1100101_2\ $ expanded into Horner form, viz.
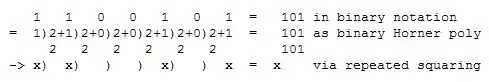
- 272,048
In the case of $25^9 \pmod{33}$ it is pretty straightforward to use exponentiation by squaring because $9 = 8 + 1 = 2^3 + 2^0$.
$25 \equiv 25 \pmod{33}$
$25^2 \equiv 31 \pmod{33}$
$25^4 \equiv 31^2 \equiv 4 \pmod{33}$
$25^8 \equiv 4^2 \equiv 16 \pmod{33}$
$25^9 \equiv 25^8 \times 25 \equiv 16 \times 25 \equiv 4 \pmod{33}$
- 25,582
- 7
- 59
- 91
- 255