If $S$ is set of lower sums for partitions having $n$-equal subintervals, does $\sup S$ equal the $\sup$ of the set of lower sums for all partitions.

Question

Firstly, here are two relevant definitions:

Let $a \lt b$. A partition of the interval $[a,b]$ is a finite collection of points in $[a,b]$, one of which is $a$ and one of which is $b$.

Suppose $f$ is bounded on $[a,b]$ and $P=\{t_0,t_1, \cdots, t_n\}$ is a partition of $[a,b]$. Let \begin{align} m_i=\inf\{f(x):t_{i-1} \leq x \leq t_i\}. \end{align} The lower sum of $f$ for $P$, denoted by $L(f,P)$ is defined as \begin{align}\displaystyle L(f,P) = \sum_{i=1}^n m_i(t_i-t_{i-1})\end{align}

---

Consider the set $\mathcal S$ of all partitions of $[a,b]$ that have $n$ equal subintervals. For example, if the interval of interest is $[0,4]$, then the partition $P=\{0,1,2,3,4\}$ is in $\mathcal S$...the partition $P=\{0,0.5,1.0,1.5,\cdots,3.5,4\}$ is in $\mathcal S$...etc. Additionally, let the set $\mathcal T$ denote the set of all possible partitions of $[a,b]$.

It can be shown that there are partitions in $\mathcal T$ that are not in $\mathcal S$: i.e. there are partitions that cannot be represented by any partition that has $n$ equal subintervals. This leads me to wonder the following:

Is it true that $\displaystyle \sup_{P \in \mathcal S} L(f,P)=\sup_{P \in \mathcal T} L(f,P)$ $\quad(*)$?

I've played around with this for a while but am having difficulties finding a scheme that works for any function.

In order to prove $(*)$, I have specifically been trying to prove that:

For any $P \in \mathcal T$, there exists a $P' \in \mathcal S$ such that $L(f,P') \geq L(f,P)$.

, which I think is the correct approach. Any suggestions or insights would be appreciated.

---

Edit: Adding some additional clarifying details to Nico Tripeny's argument

Relevant Lemma:

Let set $X$ and set $Y$ have supremums $\alpha$ and $\beta$, respectively. Suppose \begin{align}\dagger_1 \quad &\forall x \in X: \forall \varepsilon \gt 0: \exists y \in Y: x \lt y + \varepsilon \\\dagger_2 \quad &\forall y \in Y: \exists x \in X: y \leq x \end{align} then we must have that $\alpha = \beta$.

The fact that $\mathcal S \subset \mathcal T$ immediately gives us $\dagger_2$ (where the lower case variables in the lemma are representing arbitrary instances of lower sums derived from the different partitions under consideration...$X$ corresponds to all of the lower sums derived from $\mathcal T$ and $Y$ corresponds to all of the lower sums derived from $\mathcal S$). We need to prove $\dagger_1$, which Nico Tripeny's proof does in the following way (I will generalize to $[a,b]$ rather than $[0,1]$):

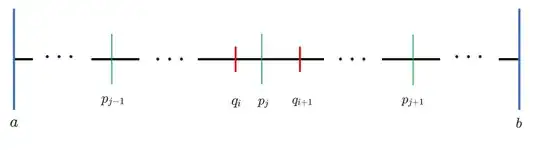
Consider a partition $P \in \mathcal T$. In order for this argument to not be trivial, suppose there exists a $p_j \in P$ that cannot be expressed as $a+i\cdot\frac{b-a}{n}$ for any $n \in\mathbb N$ and any $i \in \{0,1,\cdots, n-1,n\}$, which is equivalent to saying that $P \notin \mathcal S$. Even though $p_j\neq a+i\cdot\frac{b-a}{n}$, for a large enough $k \in \mathbb N$, I can still guarantee that there is partition $P' \in \mathcal S$ that contains consecutive members $q_i$ and $q_{i+1}$ such that $q_i \lt p_j \lt q_{i+1}$.

To see this, suppose $P$ has $n+1$ members ($n$ subintervals). Because this number is finite, one can collect all of the distances between any two consecutive members and find the smallest such distance $d \gt 0$. By the Archimedean principle, there is a $k \in \mathbb N$ such that $\frac{1}{k}\lt \frac{d}{b-a}$, which means that $\frac{b-a}{k} \lt d$. Importantly, this implies that for every subinterval of $P$, denoted by $[p_j, p_{j+1}]$, there is a $q \in P'$ such that that $q \in (p_j,p_{j+1})$.

The following picture will be useful to understanding the argument:

The next question to consider is: "How small should we make these subintervals when constructing our uniform partition?"

There are two scenarios to consider:

1. The new small subinterval from the uniform partition is contained purely within (end-point overlap allowed) a subinterval of $P \in \mathcal T$. Letting the $P$ subinterval be denoted by $[p_{j-1},p_j]$, it should be clear that new small subinterval contained within $[p_{j-1},p_j]$ has its own infimum $\geq$ the full-interval infimum on $[p_{j-1},p_j]$. Therefore, we do not need to consider these in order to prove $\dagger_1$ (as such conditions would be truthful for any $\varepsilon \gt 0$).

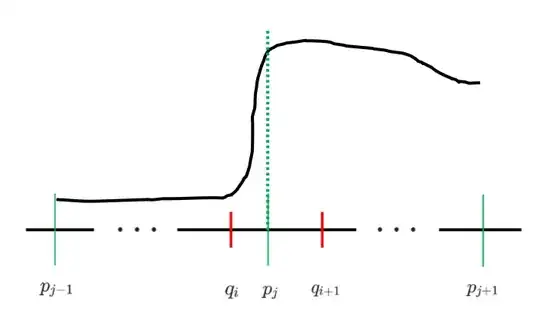
2. The new small subinterval from the uniform partition spans two consecutive subintervals from $P$ (like that depicted in the above image). For this scenario, (referencing the symbols used in the above image), it is NOT necessarily the case that the infimum of $[q_{i-1},q_i]$ is simultaneously $\geq$ the infimum of $[p_{i-1},p_i]$ and $[p_{i},p_{i+1}]$ (the counter example shown by Nico Tripeny in his one answer demonstrates this nicely). Just to make sure the idea is conveyed, consider the below image:

Although the infimum of the proposed function on $[q_{i-1},q_i]$ is $\geq$ the infimum on $[p_{i-1},p_i]$, it is clearly NOT the case for $[p_{i}, p_{i+1}]$. As such, we actually have that the infimum of $f$ on $[q_{i-1},q_i]$ is $\lt $ the infimum of $f$ on $[p_{i},p_{i+1}]$, and we need to properly account for this in order to prove $\dagger_1$. Technically, depending on the shape of $f$, it could be the case that $m_{q_{i+1},q_i} \gt m_{p_{j},p_{j-1}}$ and $m_{q_{i+1},q_i} \gt m_{p_{j+1},p_{j}}$...but, in such a circumstance, no special treatment is needed (for the same reason as case 1). So let us suppose that we are only dealing with 'bad' versions of case 2.

For this second case, recall our definition of lower sums. It is easy to see that for a given $i^{\text{th}}$ subinterval, we can rewrite the contributing sum from $m_i\cdot(t_i-t_{i-1})$ to $m_i\cdot (z-t_{i-1})+m_i\cdot(t_i-z)$ for some $z \in [t_{i-1},t_i]$. i

With this in mind and referencing our above photo, consider the contributions that the following partial intervals make to the lower sums of $L(f,P)$ and $L(f,P')$, respectively:

$$(p_j-q_i)\cdot m_{p_j,p_{j-1}}+(q_{i+1}-p_j)\cdot m_{p_{j+1},p_j}$$

and

$$(p_j-q_i)\cdot m_{q_{i+1},q_i}+(q_{i+1}-p_j)\cdot m_{q_{i+1},q_i}$$

Because we assume that $f$ is bounded (meaning $\forall x: |f(x)|\lt N$...and let $M=N+1$), we certainly know that the following must be true:

\begin{align}&\left|\left[(p_j-q_i)\cdot m_{p_j,p_{j-1}}+(q_{i+1}-p_j)\cdot m_{p_{j+1},p_j}\right]-\left[(p_j-q_i)\cdot m_{q_{i+1},q_i}+(q_{i+1}-p_j)\cdot m_{q_{i+1},q_i}\right] \right| =\\ & \left| \left[(p_j-q_i)\cdot m_{p_j,p_{j-1}}-(p_j-q_i)\cdot m_{q_{i+1},q_i}\right] + \left[(q_{i+1}-p_j)\cdot m_{p_{j+1},p_j}-(q_{i+1}-p_j)\cdot m_{q_{i+1},q_i}\right] \right| \leq \\ &\left|(p_j-q_i)\cdot m_{p_j,p_{j-1}}-(p_j-q_i)\cdot m_{q_{i+1},q_i}\right|+\left|(q_{i+1}-p_j)\cdot m_{p_{j+1},p_j}-(q_{i+1}-p_j)\cdot m_{q_{i+1},q_i}\right| \lt \\ &(p_j-q_i)2M+q_{i+1}-p_j)2M=\left(q_{i+1}-q_{i}\right)2M=\frac{b-a}{k}2M\end{align}

We thus have that:

$$\left|\left[(p_j-q_i)\cdot m_{p_j,p_{j-1}}+(q_{i+1}-p_j)\cdot m_{p_{j+1},p_j}\right]-\left[(p_j-q_i)\cdot m_{q_{i+1},q_i}+(q_{i+1}-p_j)\cdot m_{q_{i+1},q_i}\right] \right|\lt \frac{b-a}{k}2M$$...and, really, the absolute bars can be dropped because we are only dealing with the 'bad' version of case 2.

Because the partition $P$ is comprised of $n$ subintervals, the bad version of case 2 can occur at most at $n-1$ locations. Therefore, if we tally up all of these accumulated differences, we will have a difference of $\lt (n-1)\times \frac{b-a}{k}2M$.

We previously required that $\frac{1}{k} \lt \frac{d}{b-a} \quad (*_1)$. However, there is nothing from preventing us from constructing a number that is even smaller...in fact, we can make an arbitrarily small number. Therefore, let us also impose that $\frac{1}{k}\lt \frac{\varepsilon}{2M\times (n-1)\times(b-a)} \quad (*_2)$. Choose the $k$ that satisfies both $(*_1)$ and $(*_2)$. Under such circumstances, we then have that $(n-1)\times \frac{b-a}{k}2M \lt \varepsilon$.

Finally, suppose that we construct a uniform partition $P' \in \mathcal S$ that has $k$ subintervals of equal length (where $k$ adheres to our aforementioned criteria). Let $K_1$ be a collection of the various subintervals that are members of $P'$ that correspond to case 1; let $K_2$ be a collection of the various subintervals that are members of $P'$ that correspond to case 2. Note that $K_1 \cup K_2$ contains all subintervals that comprise $P'$ (and, of course, $P$). Next, let $x_1$ be the lower sum contribution of the total lower sum of $P$ that is derived from the subintervals of $K_1$; let $x_2$ correspond to the lower sum contribution of the total lower sum of $P$ that is derived from the intervals of $K_2$. It is obvious that $x_1+x_2=x$, where $x$ is the total lower sum of $P \in \mathcal T$. Let us define $y_1$ and $y_2$ similarly, but in the context of $P'$. Clearly, $y_1+y_2=y$, where $y$ is the total lower sum of $P' \in \mathcal S$.

Consider the expression $(x_1-y_1)+(x_2-y_2)$. By construction, we know that $(x_2-y_2) \lt \varepsilon$ (this positive $\varepsilon$ is a bound on how bad we undershoot the lower sum here). But we also know that $(x_1-y_1) \leq 0$. Therefore, $(x_1-y_1)+(x_2-y_2)\lt \varepsilon \iff (x_1+x_2) \lt y_1+y_2 +\varepsilon \iff x \lt y +\varepsilon$.

Note that if too few of 'bad' case 2 versions are present, then $(x_2-y_2)$ may simply be negative...in which case, $x \lt y$, and, therefore, obviously $x \lt y + \varepsilon$.

Answer 1

Unfortunately I cannot comment because I don’t have enough rep, but here is an idea of why your approach might not be working. Let $f$ from $[0,1]$ be defined so $f(x)=0$ when $x<\frac{1}{\sqrt{2}}$ and $1$ otherwise. The partition $\{0, \frac{1}{\sqrt{2}},1\}$ will give a value of $1-\frac{1}{\sqrt{2}}$. But for any value of $n$, the partitions you discuss will not include $\frac{1}{\sqrt{2}}$ so will always have a smaller value.

This doesn’t mean the statement is false of course, just that the method you suggest won’t work for the general case.

Answer 2

For continuous functions (or more generally Riemann integrable functions) it is true that $\sup_{P \in\mathcal{S}}L(P,f) = \sup_{P\in \mathcal {T}}L(P,f)$, where $\mathcal{S}$ is the set of uniform partitions and $\mathcal{T}$ is the set of all partitions.

This follows because for a Riemann integrable function, the supremum of lower sums over all partitions is the integral, viz.

$$\sup_{P \in\mathcal{T}}L(P,f) = \underline{\int}_a^b f(x) \, dx = \int_a^b f(x) \, dx $$

Now for any $L(P,f)\in \mathcal{S}$, the lower sum is bounded above as $L(P,f) \leqslant \int_a^b f(x) \, dx$. Since such lower sums over uniform partitions converge to the integral as $\|P \| \to 0$ it is easily shown that

$$\sup_{P\in\mathcal{S}}L(P,f) = \int_a^b f(x) \, dx=\sup_{P\in\mathcal{T}}L(P,f)$$

Addendum

This result is, in fact, true for any bounded function. This follows because it can be shown that for any $\epsilon > 0$ there exists $\delta > 0$ such that if the norm of the partition satisfies $\|P\| < \delta$, then the lower Darboux sum is within $\epsilon$ of the lower Darboux integral, viz.

$$\tag{*}\underline{\int}_a^b f(x) \, dx - \epsilon< L(P,f) \leqslant\underline{\int}_a^b f(x) \, dx$$

A proof of this fact is indicated here.

Since,

$$\underline{\int}_a^b f(x) \, dx = \sup_{P \in \mathcal{T}}L(P,f),$$

we have, using (*), for any uniform partition $P \in \mathcal{S}$ with $\|P\| < \delta$,

$$\sup_{P \in \mathcal{T}}L(P,f)-\epsilon< L(P,f) \leqslant \sup_{P \in \mathcal{S}}L(P,f) \leqslant \sup_{P \in \mathcal{T}}L(P,f)$$

Since $\epsilon$ can be arbitrarily close to zero it follows that $$\sup_{P \in \mathcal{S}}L(P,f) = \sup_{P \in \mathcal{T}}L(P,f)$$

Answer 3

Here is a (sketch of a) solution to the question. Assume $f:[0,1]\to\mathbb{R}$ is bounded so that $|f(x)|<M$ for all $x$ in the domain. It suffices to show that for all $P\in\mathcal{T}$ and all $\varepsilon$, there is a $P'\in \mathcal{S}$ such that $L(f,P)<L(f,P')+\varepsilon$. Let $l$ be the number of elements in $P$, then make $n > \frac{2lM}{\varepsilon}$ where $n$ is the number of elements in $P'$.

We see that most intervals in $P'$ will be completely within those of $P$, except for maybe $l$, as this is the number of points in $P$. If the interval is inside one from $P$, then we can ignore it as the value it adds to the sum will be greater then or equal to the what that section adds in $P$. By boundedness, the intervals in $P'$ that intersect those in $P$ can only have an infimum $2M$ smaller than the corresponding part of $P$. Using this and that there are only $l$ such intervals, we see $L(f,P)<L(f,P') + 2lM\frac{\varepsilon}{2lM}= L(f,P')+\varepsilon$.

The basic idea is once the partitions in $\mathcal{S}$ are fine enough, almost all intervals fall within the intervals in $P$ for a general partition. So the values of the lower sum become very close together.