1

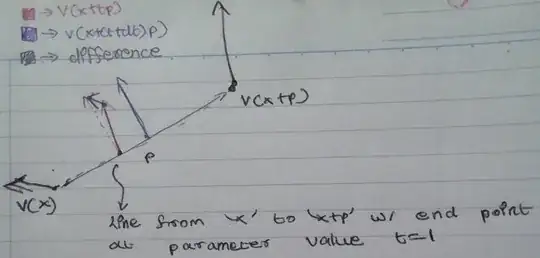
In Chapter 2 of Numerical Optimization by Nocedal and Wright, the authors have written the following equation:

$$ \nabla f(\overrightarrow x + \overrightarrow p) = \nabla f(\overrightarrow x) + \int_0^1 \nabla^2 f(\overrightarrow x + t\overrightarrow p)\overrightarrow pdt $$

where $f:R^n \rightarrow R$ is twice continuously differentiable, and $\overrightarrow p \in R^n$.

What I think the integral means is - compute the integral element-wise for each entry in the $nx1$ column vector that results from left-multiplying the Hessian of $f$ at $(\overrightarrow x + t\overrightarrow p)$ by $\overrightarrow p$. Is this correct?

Moreover, how is this derived as a consequence from Taylor's Theorem? I have not been able to figure out how to make that jump and was struggling with the notation of integrating over a vector in this manner.

simple_machine
  • 9

2 Answers2

1

Yes, integration of vector-valued functions is performed element-wise.

For your second question, say you have a continuously differentiable function $F:\mathbb{R}^n\rightarrow\mathbb{R}^n$ and you want to find the derivative of the function $G: \mathbb{R}\rightarrow \mathbb{R}^n$ given by $G(t) = F(x+tp)$. Using the chain rule you get $$G\,'(t) = \nabla F(x+tp) \,(x+tp)' = \nabla F(x+tp) \,p.$$ In other words $G(t)$ is the antiderivative of $\nabla F(x+tp)\, p$ so you can write: $$ G(1)-G(0) = F(x+p) - F(x) = \int^1_0{\nabla F(x+tp)\, p}\,\text{dt} $$ The result in the book is obtained by taking $F = \nabla f$.

camilo
  • 81
0

Picture:

enter image description here

The idea is to first consider a line from $x$ to $ x +p$ , and write down the following equation:

$$ v(x + (t+ dt) p ) - v(x +tp ) = \nabla_{pdt} v$$

The right most side is the directional derivative of $v$ in $p$ dt. Summing this expression over all the individual time partitions (while making time partition small), we have:

$$ v(x+p) - v(x) = \int_{t=0}^{t=1} \nabla_{pdt} v = \int_{t=0}^{t=1} (\nabla v) p dt$$

Note that here I am taking gradient of a vector. See here for more information.

tryst with freedom
  • 11,538