Calculate the probability P(X $\ge$ Y)

Question

I've been given the following exercise:
Given the function $$ \rho(x,y) = \left\{ \begin{array} \\cxy &,\ x \ge 0,\ 1-x \ge y \ge 0 \\ 0 &, \ elsewhere \\ \end{array} \right. $$

a) Find $c$ so that $\rho$ is a probability density function (calculated to be 24).
b) Calculate $P( X \le \frac{1}{2}, \ Y \le \frac{1}{4})$. I've solved this one too.
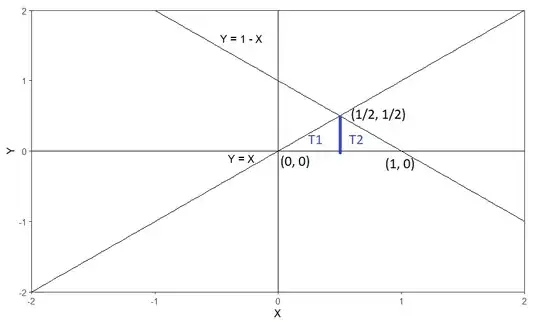
c) Calculate the probability $P(X\ge Y)$

It's the last question where I get stuck. I've tried to do this method but it requires the two random variables be independent functions.
I've tried integrating them to get the functions $(f_x(x) = \int\rho(x,y)\ dy)$ but applying what I get to the method above doesn't give me sensical results.

Any and all answers are appreciated, thank you.

Considering all constraints on $x$ and $y$ the integral in (c) should be $\int_0^1 \int_0^{\min(1-x,x)}cxy dydx$. — Kurt G., May 08 '22 at 18:30
The link you provided refers to the question, not to a particular answer. If the question mentions independence, that does not necessarily mean that every answer requires it. — paperskilltrees, May 08 '22 at 18:31
Changed link to point to answer instead of question, sorry for the confusion. — Giannis Koulouras, May 08 '22 at 18:39
since $\rho (x,y)$ is symmetric in $x,y$ and so is the the definition domain, then $P(X \ge Y)=P(Y \ge X) = 1/2$ — G Cab, May 08 '22 at 19:19

score 2 · Accepted Answer · answered May 08 '22 at 19:25

The region of integration of $\rho$ is given by the red below.

Consider, in addition, the line $Y = X$. The region for which $Y \leq X$ is given by the green.

The intersection of the red and green regions will give you the appropriate region of integration to calculate $P(Y \leq X)$, given in blue:

My suggestion would be to partition this triangle into two regions $T_1$ and $T_2$:

The intersection of the two lines occurs when $X = 1 - X$, or $2X = 1$, or $X = 1/2$, where $Y = 1/2$ as well. I have also included other points worth noting.

The region $T_1$ is given by $X$-bounds of $0$ and $1/2$, and $Y$-bounds of $0$ and $X$.

The region $T_2$ is given by $X$-bounds of $1/2$ and $1$, and $Y$-bounds of $0$ and $1 - X$.

Therefore, the desired probability is given by $$\int_{0}^{1/2}\int_{0}^{x}\rho(x, y)\text{ d}y\text{ d}x + \int_{1/2}^{1}\int_{0}^{1-x}\rho(x, y)\text{ d}y\text{ d}x = \dfrac{1}{2}\text{.}$$

I will leave the integration details to you.

Calculate the probability P(X $\ge$ Y)

1 Answers1