Interesting Pattern in Square Numbers and Pattern for Cube Numbers

Question

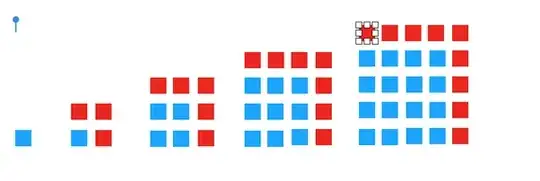
I am absolutely not the first person to notice this, but I did notice that the difference between any two squares increases by 2, starting at 1(between $0^2$ and $1^2$). I am not the best at explaining, but it can be summarized in the equation below, where n is the number to be squared.

$n^{2}=\sum_{k=1}^{n}\left(2\left(k-1\right)+1\right)$

This isn't necessarily a question at all, just something I wanted to share. But there is a sort of question within this.

I have attempted to create a similar equation for cube numbers, and while I've gotten decently close, I haven't gotten there. I would imagine the equation would be similar to something like this: $n^{2}=\sum_{k=1}^{n}\left(6\left(k-1\right)+1\right)$ However, it doesn't work. I was wondering if anyone else could make an equation for this, although I don't expect anyone to. I noticed the difference between cube numbers was 6 instead of 2 for squares, but simply replacing 2 with 6 doesn't work. It could be due to something about how cube numbers work, as there is an added layer of multiplication, I don't know if that would make a difference. Anyway, have a good day. :)

Answer 1

I think you mean

$$n^3 = \sum_{k=1}^n (k^3 - (k-1)^3) = \sum_{k=1}^n (3 k^2 - 3 k + 1)$$

Answer 2

Good job taking the first step to being a mathematician - making observations :)

Your first pattern is indeed correct: $n^2 = \sum_{k=1}^n 2k - 1$. Writing out the equations for first few $n$:

$$\begin{align*} n = 1 &\implies 1^2 = 1 \\ n = 2 &\implies 2^2 = 1 + 3 \\ n=3&\implies 3^2=1+3+5\\n=4&\implies 4^2=1+3+5+7 \end{align*}$$

In other words, the sum of the first $n$ odd number is precisely $n^2$. It is nicely demonstrated in this picture I stole online:

Now stare at this photo. How can we derive the red layer without guessing patterns? Well, notice that the $n$th red layer consists of $n^2 - (n - 1)^2$ squares, which with a bit of algebra gives $2n - 1$ squares, precisely the summed term $2k - 1$ you got. Indeed, if we add up the first $n$ red layers, we will get the entire $n$th square.

With this, we can derive a similar formula for $n^3$. Consider an abstract object (also known as a "cube") with $n^3$ "units" in the $n$th picture. The corresponding red layer will consist of

$$n^3 - \underbrace{(n - 1)^3}_{\text{previous layer (blue tiles)}} = n^3 - (n^3 - 3n^2 + 3n - 1) = 3n^2 - 3n + 1$$

What this means is that if we sum up $\sum_{k=1}^n (3k^2-3k+1)$, we will get $n^3$. In other words,

$$n^3 = \sum_{k=1}^n 3k^2-3k+1$$

This also explains why you couldn't find a linear summing pattern for $n^3$ - it does not exist!

In general, sum of degree $n$ polynomials will give a degree $n + 1$ polynomial - read more about Faulhaber's formula.

Answer 3

Here is a different summation that handles not just squares and cubes, but higher powers as well. It works by using carefully selected indices of summation, rather than trying to find a sum that runs from $1$ to $n$. The following formula describes a sequence of $n$ consecutive odd numbers that sum to $n^k$ for any $n,k$: $$\sum_{i=\frac{n^{k-1}-n}{2}+1}^{\frac{n^{k-1}+n}{2}}(2i-1)$$ The sum contains $n$ members whose average value is $n^{k-1}$; hence the sum is $n\cdot n^{k-1}=n^k$

If you set $k=2$, this reduces to the observation you have made. $$\sum_{i=1}^{n}(2i-1)$$

The pattern obtained for cubes is interesting and unique: $$1^3=1 \\2^3=3+5 \\3^3=7+9+11 \\4^3=13+15+17+19 \\\dots$$

For both squares and cubes, every odd number is an addend in at least one sum. This is not the case for higher powers.