9

Is the limit $$ e^{-x}\sum_{n=0}^N \frac{(-1)^n}{n!}x^n\to e^{-2x} \quad \text{as } \ N\to\infty \tag1 $$ uniform on $[0,+\infty)$?

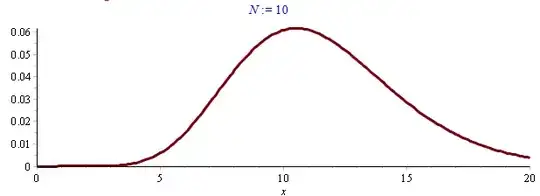
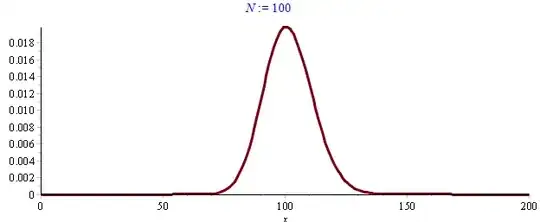
Numerically this appears to be true: see the difference of two sides in (1) for $N=10$ and $N=100$ plotted below. But the convergence is very slow (logarithmic error $\approx N^{-1/2}$ as shown by Antonio Vargas in his answer). In particular, putting $e^{-0.9x}$ and $e^{-1.9x}$ in (1) clearly makes convergence non-uniform.

One difficulty here is that the Taylor remainder formula is effective only up to $x\approx N/e$, and the maximum of the difference is at $x\approx N$.

N=10

enter image description here

The question is inspired by an attempt to find an alternative proof of $\epsilon>0$ there is a polynomial $p$ such that $|f(x)-e^{-x}p|<\epsilon\forall x\in[0,\infty)$.

Community
  • 1
40 votes
  • 9,736
  • I have no time to give a full answer at this moment, but I think this post, in particular my answer there and Stirling's formula are enough to prove your statement. – 23rd Jul 14 '13 at 19:36
  • @Landscape Julien says my idea might be what you had in mind. Care to take a look? – Pedro Jul 14 '13 at 22:12
  • 1
    @PeterTamaroff: What I intended to say is as follows. For $r_n(x)=e^{-x}-\sum_{k=0}^n\frac{(-1)^kx^k}{k!}$ with $x>0$, from $r_{n-1}(x)\cdot r_n(x)<0$ we know that $|r_{n-1}(x)|<|r_{n-1}(x)-r_n(x)|=\frac{x^n}{n!}$. Then it suffices to estimate $f_n(x)=e^{-x}\frac{x^n}{n!}$. $f_n'(x)=0\iff x=n$, so $0<f_n(x)\le f_n(n)$, and the conclusion follows from Stirling's lemma. However, it turns out that $|r_{n-1}(x)|<\frac{x^n}{n!}$ follows from Taylor's expansion of $e^{-x}$ at $x=0$ with Lagrange form of the remainder immediately, so the observation $r_{n-1}(x)\cdot r_n(x)<0$ is not necessary. – 23rd Jul 15 '13 at 03:18
  • @Landscape I will try to make my answer more meaningful by imitating your ideas. Thank you. – Pedro Jul 15 '13 at 03:31
  • @PeterTamaroff: You are welcome. I will be glad to see your updated answer. – 23rd Jul 15 '13 at 03:40
  • @Landscape I think it is nonsensical to try to obtain a simpler argument than the one above, thus I will add that to my answer and properly attribute you for it. If you'd like to answer on your own, I can just delete it and worry about what this question gave rise to. – Pedro Jul 15 '13 at 03:56
  • @PeterTamaroff: Please feel free to edit your answer. :) – 23rd Jul 15 '13 at 03:59

3 Answers3

5

Credits should go to Landscape.

Define $$r_n(x)=\sum_{k=n+1}^\infty (-1)^k\frac{x^k}{k!}$$

Note that by Taylor's theorem with Lagrange's form of the remainder we can write $$r_n(x)=(-1)^{n+1}e^{-x'}\frac{x^{n+1}}{(n+1)!}$$

where $x'$ is positive. It follows $$e^{-x}|r_n(x)|\leq e^{-x}\frac{x^{n+1}}{(n+1)!}$$

Easy verification shows the last function has absolute maximum at $x=n+1$. But $$\frac{1}{{(n + 1)!}}{\left( {\frac{{n + 1}}{e}} \right)^{n + 1}} \sim \frac{1}{{\sqrt {2\pi \left( {n + 1} \right)} }}$$ by Stirling, so convergence is indeed uniform. $\quad \Box$

Community
  • 1
Pedro
  • 122,002
5

Thanks, this was a fun problem.

From the integral representation

$$ \sum_{k=0}^{n} \frac{x^k}{k!} = \frac{1}{n!} \int_0^\infty (x+t)^n e^{-t} \,dt \tag1 $$

we can derive the expression

$$ e^{-x} \sum_{k=0}^{n} \frac{(-x)^k}{k!} = e^{-2x} - \frac{e^{-2x} (-x)^{n+1}}{n!} \int_0^1 t^n e^{xt}\,dt. \tag2 $$

Now

$$ \int_0^1 t^n e^{xt}\,dt \leq e^x \int_0^1 t^n\,dt = \frac{e^x}{n+1}, \tag3 $$

so that

$$ \begin{align} \left|\frac{e^{-2x} (-x)^{n+1}}{n!} \int_0^1 t^n e^{xt}\,dt\right| &\leq \frac{e^{-x} x^{n+1}}{(n+1)!} \\ &\leq \frac{e^{-n-1} (n+1)^{n+1}}{(n+1)!} \\ &\sim \frac{1}{\sqrt{2\pi n}} \end{align} \tag4 $$

by Stirling's formula.

Added by 40 votes for those interested in the derivation of (2) from (1): $$ \sum_{k=0}^{n} \frac{(-x)^k}{k!} = \frac{1}{n!} \int_0^x (t-x)^n e^{-t} \,dt + \frac{1}{n!} \int_x^\infty (t-x)^n e^{-t} \,dt \tag{A} $$ Substitute $u=t-x$ in the second integral on the right of (A): $$\frac{1}{n!}\int_x^\infty (t-x)^n e^{-t} \,dt =\frac{1}{n!}\int_0^\infty u^n e^{-u-x} \,dt = e^{-x} \tag{B}$$ Substitute $u=1-t/x$ in the first integral on the right of (A), noting that $(t-x)^n=(-x)^n u^n$ and $dt=(-x)du$: $$\frac{1}{n!} \int_0^x (-x+t)^n e^{-t} \,dt = \frac{(-x)^{n+1}}{n!} \int_0^1 u^n e^{xu-x} \,du = \frac{e^{-x}(-x)^{n+1}}{n!} \int_0^1 u^n e^{xu} \,du \tag{C} $$ Adding (B) and (C), identity (2) follows.

40 votes
  • 9,736
Antonio Vargas
  • 24,993
  • 1
    Interestingly, your integral representation shows that we can estimate the remainder by $\frac{e^{-x}x^{n+1}}{(n+1)!}$ just as if we had said that $\Big|\sum_{k\geq n+1}\frac{(-x)^k}{k!}\Big|\leq \frac{x^{n+1}}{(n+1)!}$ by invoking Leibniz criterion (which unfortunately requires $n>x$ here, whence can't be uniform). +1. – Julien Jul 14 '13 at 21:57
  • Wonderful answer! Having spent several minutes figuring out the transition (1)->(2), I added it in case others are doing the same. – 40 votes Jul 15 '13 at 01:01
  • @40votes Thank you :). Sometimes I have a habit of leaving maybe a bit too much to the reader. – Antonio Vargas Jul 15 '13 at 01:19
  • Moved the checkmark because Landscape and Peter came up with an embarrassingly simple answer. :) – 40 votes Jul 15 '13 at 16:17
1

I'd like to provide another solution which is a mixture of Antonio's and Landscape's. One can also write $$\left|r_n(x)\right|=\int_0^x {e^{-t}}\frac{(x-t)^n}{n!}dt$$

by virtue of Taylor's theorem with the integral remainder. But then again $$\left| {{r_n}(x)} \right| \leqslant \int_0^x {\frac{{{{(x - t)}^n}}}{{n!}}dt} = \int_0^x {\frac{{{u^n}}}{{n!}}du} = \frac{x^{n + 1}}{{\left( {n + 1} \right)!}}$$

and Strling does the job.

Pedro
  • 122,002