Inverting a cubed root equation with two cube roots

Question

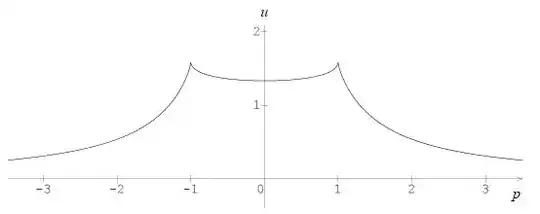
In a recent StackOverflow question, I came across this formula:

$$up = (1 + p)^\frac{2}3 - (1 - p)^\frac{2}3 $$

and the question required the poster to plot p as a function of u. I misunderstood the question and thought it was just a simple dividing both sides by p.

Upon being corrected, I realized that I had to change the formula such that it would be p=f(u).

I tried the following:

First try:

$$up + (1 - p)^\frac{2}3 = (1 + p)^\frac{2}3$$

Cube both sides:

$$(up + (1 - p)^\frac{2}3)^3 = (1 + p)^2$$

Expanding the left:

$$ (up)^3 + 3(up)^2(1 - p)^\frac{2}3 + 3(up)(1 - p)^\frac{4}3 + (1 - p)^2 = (1 + p)^2$$

At this point, I stopped and realized that if I were to proceed with singling out the cubed roots, I'd get even more terms with cubed roots.

So, 2nd try:

Let $a = (1 + p)^\frac{1}3$ and $b = (1 - p)^\frac{1}3$, so $p = a^3 - 1$ or $p = 1 - b^3$.

So I get: $$u(a^3 - 1) = a^2 - b^2$$

Then:

$$a^2 - u(a^3 - 1) = b^2$$

I'm not even sure this is the right approach as it's just as complicated and doesn't help me.

So I firstly had to understand what it meant to a function having an inverse.

To re-acquaint myself with this simply basic concept (haven't done any 'hard'(very relative) maths in some time), I came across this link)

  A function, f(x) has an inverse function if f(x) is one-to-one

The original question is just: $yx = (1 + x)^\frac{2}3 - (1 - x)^\frac{2}3$

So,

$$y = \frac{1}x [(1 + x)^\frac{2}3 - (1 - x)^\frac{2}3]$$

I had thought to prove that this function is one to one (i.e. assume $a \not= b$ and $f(a) = f(b)$ and arrive at a conclusion of RAA) as follows:

Assume a and b are in the domain, and $a \not= b$ but $f(a) = f(b)$.

So

$$\frac{1}a ((1 + a)^\frac{2}3 - (1 - a)^\frac{2}3) = \frac{1}b ((1 + b)^\frac{2}3 - (1 - b)^\frac{2}3)$$

Which after some basic algebraic manipulation:

$$b(1 + a)^\frac{2}3 + a(1 - b)^\frac{2}3 = a(1 + b)^\frac{2}3 + b(1 - a)^\frac{2}3$$

Which seems like a rabbit hole in itself.

At this point, I tried the following code:

def sq(in_v):
    return (in_v ** 2) ** (1.0 / 3.0)
def f(x):
    retval = 0
    if x != 0:
        ux = float(x)
        retval = (1.0 / ux) * ((sq(1.0 + ux) - sq(1.0 - ux)))
    return retval
for i in range(1, 1000):
    print(i, f(i))

Which outputted:

(1, 1.5874010519681994)
(2, 0.540041911525952)
(3, 0.31081368260718234)
(4, 0.2109834787902405)
(5, 0.156417029820976)
(6, 0.12254799530168421)
(7, 0.09972467872933903)
(8, 0.08343037511240664)
(9, 0.07128764817919765)
(10, 0.06193387323264759)
(11, 0.05453581407318313)
(12, 0.04855728086918091)
(13, 0.04363868808814697)
(14, 0.039530512992466287)
(15, 0.0360545649539396)
(16, 0.03308043893028406)
(17, 0.030510661614540784)
(18, 0.028271018913558234)
(19, 0.026304081155830626)
(20, 0.024564762605912584)
(21, 0.023017210155186492)
(22, 0.021632581275900904)
(23, 0.020387429637735967)
...

Which seems like the i'th value isn't the same as the (i+1)th value. So I'm guessing there is an inverse function. (This is also assuming I even programmed this correctly).

At this point, it is unclear on how I can proceed to find the inverse function.

My mind's so blank right now, I'm not sure how to proceed or even if I'm just barking up the wrong tree and that I misunderstood the question entirely (of which I apologize).

Can someone please clarify where I went wrong? My lack of maths practice has severely degraded my maths.

I appreciate the help,

Answer 1

There is an analytical inverse of $$y = \frac{ (1 + x)^\frac{2}3 - (1 - x)^\frac{2}3}x$$ After a tedious series of cubing steps, $x$ is the solution of $$y^9 \,x^6+3 y^3 \left(9-4 y^3\right)\,x^4-6 y^3\,x^2+\left(27 y^3-64\right)=0$$ which is a cubic in $x^2$.

Since $\frac{4}{3}<y<2^{2/3}$, the discriminant of the cubic is positive. Using the trigonometric method for three real roots, then $$x^2=\frac{4 y^3-9+6 \sqrt{2 y^6-8 y^3+9}\,\, \sin \left(\frac{1}{3} \sin ^{-1}\left(\frac{\left(y^3-4\right) \left(y^6-4 y^3+18\right) y^3+54}{2 \left(2 y^6-8 y^3+9\right)^{3/2}}\right)\right)}{y^6}$$ Consider the two branches $$x_\pm=\pm \sqrt{\frac{4 y^3-9+6 \sqrt{2 y^6-8 y^3+9}\,\, \sin \left(\frac{1}{3} \sin ^{-1}\left(\frac{\left(y^3-4\right) \left(y^6-4 y^3+18\right) y^3+54}{2 \left(2 y^6-8 y^3+9\right)^{3/2}}\right)\right)}{y^6} }$$ to have the whole curve.

Answer 2

This answer was actually answered by @CalvinKhor but he allowed me to post it. I am attempting to summarize what @CalvinKhor posted.

As a summary to my question, the original function isn't a one-to-one function. My post's 'cheat' used a script to generate values from (1 to 1000); but, I failed to include the negative portion of the X axis. Had I included it, I'd have found out that the function wasn't one-to-one, (and allowed me to avoid stressing over figuring out the 'inverse' manually).

That said, as @CalvinKhor pointed out:

1. The original function has an inverse on a 'restricted domain'; that is $x\in(0, 1]$
2. There is a finite value at x = 0 as the limit exists as $x \to0$
3. The singularity is removeable and
4. There is a continuous extension. [* - will need to research this as I'm not familiar with this term]

So in conclusion, the original function $up = (1 + p)^\frac{2}3 - (1 - p)^\frac{2}3$ has an inverse in the domain of $x\in(0, 1]$ and this inverse function (where valid) could be set as: $$x = \frac{(1 + y)^\frac{2}3 - (1 - y)^\frac{2}3)}y$$

My thanks to @CalvinKhor for the help. Any errors in the above answer is attributable to my ignorance and misunderstandings in the explanations provided and not to @CalvinKhor's actual answer. I apologize for any mistakes made.

Answer 3

$$u(p) = \frac{1}{p}\left((1 + p)^\frac{2}3 - (1 - p)^\frac{2}3 \right)$$

I am not sure to well understand what you are looking for. Sorry if my answer is not what you want.

If the question is only to plot $u(p)$ and nothing more, this seems too obvious : In your drawing software replace plot(p,u) by plot(u,p). Which means that for each point (p given and u computed) draw the pixel (u,p) i.e. abscisse=u and ordinate=p.

If you cannot do that, first plot $u(p)$ : next figure.

Then draw the symetric curve wrt the first bisectrice : next figure

I don't see any need to analytically solve the equation for $u$.

Note : The figures have been corrected ( There was a bug in the code for drawing them).