Find a point on triangle and interpolated triangle normal which points to specific point in 3D

Question

Suppose i have triangle in 3d with vertices $v1, v2, v3 \in R^3$. Each triangle vertex has associated normal vector $ n1, n2, n3 \in R^3, ||n_i|| = 1$. In computer graphics such vectors sometimes called smooth normals. By interpolating such normals it's possible to obtain approximation to real surface normal in the middle of triangle (I attached the picture for clarity).

Suppose i also have a point somewhere near my triangle $p \in R^3$. How i can find such position on triangle and interpolated normal so resulting ray points to my point $p$?

I can formulate my problem as solution of this system of equations and inequalities:

$$ v1 * b1 + v2 * b2 + v3 * (1 - b1 - b2) + k * (n1 * b1 + n2 * b2 + n3 * (1 - b1 - b2)) = p \\ b1>=0 \\ b2 >=0 \\ b1 + b2 <= 1 \\ k >= 0 $$

Where $b1, b2, k \in R$ - my variables, $b1, b2$ - barycentric coordinates.

But i have no idea how to solve it without numerical methods.

Please feel free to ask additional information or to correct me

Answer 1

Not a complete solution, but the ideas are there...

Your vector equation, that I write with barycentric coordinates $b_1,b_2$ replaced by $x,y$:

$$v_1\cdot x + v_2 \cdot y + v_3 \cdot (1 - x - y) + k \cdot (n_1\cdot x + n_2 \cdot y + n_3 \cdot (1 - x - y)) = p$$

is equivalent to 3 scalar equations from which we can, for each of them, "extract" $k$ under the following (still equivalent) form :

$$k=\underbrace{\dfrac{ax+by+c}{dx+ey+f}}_{f_1(x,y)}=\underbrace{\dfrac{gx+hy+i}{jx+ky+l}}_{f_2(x,y)}=\underbrace{\dfrac{mx+ny+o}{px+qy+r}}_{f_3(x,y)}\tag{1}$$

with known coefficients $a,b,\cdots q,r$.

Otherwise said,

$$\begin{cases}f_1(x,y)&=&f_2(x,y)\\ f_2(x,y)&=&f_3(x,y)\\ f_3(x,y)&=&f_1(x,y)\end{cases}\tag{3}$$

These three 2nd degree equations represent conic curves. Please note that the third equation is redundant ; in fact it will be useful to select among the solutions to the system formed by the two first equations

Therefore, your issue amounts to find the intersection(s) of 2 conic curves.

Here is an example of (2) obtained with Geogebra (the coefficients have been arbitrarily chosen...) with a single solution (the intersection point of an ellipse and two hyperbolas) ; please note that if consider only two of the 3 conic curves, we have two solutions.

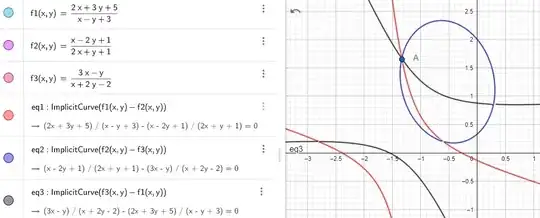
Now, out of that, which kind of strategy of resolution can we adopt ? I see two of them:

• either apply two-dimensional Newton-Raphson's method with its efficiency but as well its known drawbacks, mainly the difficulty to find a good initialization point (maybe you can orthogonaly project point $P$ on the triangle for having this initial point ?).

• or get the 4th degree equation (degree $2 \times$ degree $2$ = degree $4$) verified by variable $x$ by elimination of $y$ between the 2 first equations of (1). See the answer here for that. In fact, one can work with a 3rd degree equation as shown in this answer. Once a solution $x^*$ has been obtained, just plug $ x=x^*$ into the equations in (1) to get quadratic equations for variable $y$ giving solution(s) $y=y^*$. Plugging $x=x^*$ and $y=y^*$ in any of the two relationships (1) gives the value of $k$.

Which of the two methods is the best one ?

The advantage of the second method is that you shouldn't be exposed to particular cases where Newton's method can "wander" instead of finding the root.

---

Edit (2022-04-22): There is a possible simplification of fractions (1).

It rests on the fact that, when 3 fractions are equal, they are equal to any other fraction whose numerator and denominator are barycentric combinations of the numerators and denominators of the 3 initial fractions . The corresponding formula: for (almost) any constants $u,v,w$ :

$$\frac{A}{B}=\frac{C}{D}=\frac{E}{F}=\frac{uA+vC+wE}{uB+vD+wF}$$

In our case, considering (1), it is equal to:

$$k=\dfrac{u(ax+by+c)+v(gx+hy+i)+w(mx+ny+o)}{u(dx+ey+f)+v(jx+ky+l)+w(px+qy+r)}=\dfrac{uc+vi+wo}{u(dx+ey+f)+v(jx+ky+l)+w(px+qy+r)}\tag{3}$$

the second fraction has a purely numerical numerator if we choose $u,v,w$ in such a way that the $x$ and $y$ terms disappear ; this is always possible because equations:

$$\begin{cases}ua+vg+wm&=&0\\ub+vh+wn&=&0\end{cases}$$

have a solution ($(u,v,w)$ proportional to cross product of $(a,g,m)$ and $(b,h,n)$);