I need to show that $\sin(\frac{x}{n}) \frac{n}{x} \leq 1$. I know that this is equivalent as showing that $\frac{\sin(a)}{a} \leq 1$ with $a = \frac{x}{n}$, however I don't know how to show this. If $|a| > 1$ this is easy, and I know the limit when $a$ tends to $0$, but how can I show that this is true for all $a$ with absolute value between $0$ and $1$?
Asked
Active
Viewed 50 times
1 Answers
1
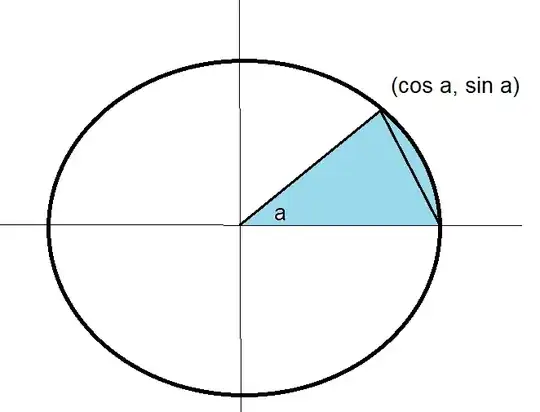
The area of the triangle is $\frac 12 |\sin a|$ The area of the section of the circle is $\frac 12 |a|.$
$|\sin a| \le |a|$
user317176
- 11,017
a \cdot bto get $a \cdot b$,a \times bto get $a \times b$ or simple juxtaposition, as you did in the body of the question. – jjagmath Mar 18 '22 at 23:31