I want to find the entropy solution of $$\frac{\partial u}{\partial t} + \frac{\partial }{\partial x}\left(\sin^2\left(\frac{\pi u}{2}\right)\right)=0$$ with $$u(x,0)=\begin{cases} 0 & \text{ if } x<0 \\ 1 & \text{ if } x>0 \end{cases}$$
I found the characteristics , $x=x_0$ if $x_0$ is not zero
Here I got confused what to do. Is the point $(0,0)$ considered a shock point or is there a rarefaction wave solution at it ?
Let us rewrite the PDE as follows $$ u_t + f(u)_x = 0, \qquad f(u) = \sin^2\left(\tfrac{\pi u}2\right) . $$ Other answers have already shown that base characteristics do not intersect given that $$ f'(0) = 0 = f'(1), \qquad f'(u) = \tfrac{\pi}{2} \sin (\pi u) . $$ Since the Rankine-Hugoniot (RH) shock speed is given by $$ s = \frac{f(1) - f(0)}{1 - 0} = 1 , $$ we conclude that the Lax entropy condition for shock wave solutions is not satisfied. Therefore, it turns out that the shock wave with RH speed $s=1$ is no entropy solution in the usual sense, neither is the static shock solution which contradicts RH.
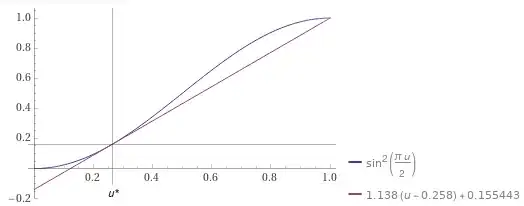
It should be noted that the function $u \mapsto f(u)$ possesses an inflection point. In other words, the Lax entropy condition is no longer relevant, and we need to look at the Oleinik entropy condition instead (see this post). The figure below shows the lower convex hull of the graph of $f$, as described in the solution construction method of the linked post. We find that the entropy solution is a semi-shock, more precisely a rarefaction-shock wave with expression $$ u(x,t) = \begin{cases} 0 , & x \leq 0 \\ \tfrac1\pi \arcsin\left(\tfrac{2}{\pi} \frac{x}{t}\right) , & 0\leq x < s^* t \\ 1 , & s^* t < x \end{cases} $$ where $u^* \approx 0.258$ satisfies $$ f'(u^*) = \frac{f(1) - f(u^*)}{1 - u^*} = s^* \approx 1.138 . $$
The essential trick in the method of characteristics is that the solution $u$ stays (by definition of a characteristic curve) constant along the characteristic curve $x(t)$: $$ \frac{\mathrm d }{\mathrm d t} u\big(x(t),t \big) = \partial_t u + \partial_x u \cdot \frac{\mathrm d x}{\mathrm d t} \overset{!}{=} 0 \\ \Rightarrow u\big(x(t), t) = u_0\big(x(t), t\big).$$ By comparing with the PDE $$u_t + \partial_x f(u) = u_t + f'(u) \cdot u_x = 0$$ you obtain $$ \frac{\mathrm d x}{\mathrm d t} = f'\Big( u\big(x(t), t\big) \Big) = f'\Big(u_0\big(x(t), t\big) \Big) = f'\Big(u_0\big(x_0(x(t), t)\big) \Big).$$ In your case: $$ f'(u_0) = 2 \sin \left( \frac{\pi u_0}2 \right) \cdot \frac \pi2 \cos \left( \frac{\pi u_0}2 \right) = \pi \sin \left( \frac{\pi u_0}2 \right) \cdot \cos \left( \frac{\pi u_0}2 \right).$$ Thus, $$ \frac{\mathrm d x}{\mathrm d t} = \begin{cases} \pi \sin \left( \frac{\pi \cdot 0}2 \right) \cdot \cos \left( \frac{\pi \cdot 0}2 \right) = \pi \cdot 0 \cdot 1 = 0, & x_0 < 0 \\ \pi \sin \left( \frac{\pi \cdot 1}2 \right) \cdot \cos \left( \frac{\pi \cdot 1}2 \right) = \pi \cdot 1 \cdot 0= 0, & x_0 > 0 .\end{cases}$$ So the characteristic curves are in both cases given by $$x(t) = x_0 , $$ i.e., they do not intersect and the solution reads $$u(x, t) = u\Big(x_0\big(x(t), t \big) \Big) = u_0(x) = \begin{cases} 0, & x< 0 \\ 1, & x > 0. \end{cases} $$
