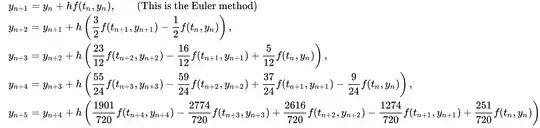In the Numerical Analysis by Richard L. Burden, section $5.4$ was told that
The first step in deriving a Runge-Kutta method is to determine values for $a_{1}, \alpha_{1}$, and $\beta_{1}$ with the property that $\color{red}{a_{1} f\left(t+\alpha_{1}, y+\beta_{1}\right)}$ approximates $$ T^{(2)}(t, y)=f(t, y)+\frac{h}{2} f^{\prime}(t, y) $$ with error no greater than $O\left(h^{2}\right)$, which is the same as the order of the local truncation error for the Taylor method of order two. And for higher order Runge-kutta methods the term $T^{(3)}(t, y)$ can be approximated with error $O\left(h^{3}\right)$ by an expression of the form $$ \color{red}{f\left(t+\alpha_{1}, y+\delta_{1} f\left(t+\alpha_{2}, y+\delta_{2} f(t, y)\right)\right)}, $$ involving four parameters, the algebra involved in the determination of $\alpha_{1}, \delta_{1}, \alpha_{2}$, and $\delta_{2}$ is quite involved.
$(1)$ I don't understand how they guess the expression like that? [red colored] Is there any logic behind this? Without understanding, it's like memorizing the derivation.
$(2)$ Another question is from linear multistep methods. Is there any way to quickly come up with the coefficient of those methods, like for $3$ step method, the coefficients $\frac{23}{12},-\frac{16}{12}$ and $\frac{5}{12}$. It's hard to memorize and can't derive the whole formula in exam time.
Adams–Bashforth methods
Adams–Moulton methods
