Question about the proof that a countable union of countable sets is countable

Question

Can One explain me a bit about the Hence

---

2.12 Theorem

Let $\{E_n\}$, where $n=1,2,3,...$, be a sequence of countable sets, and put

$S=\underset{n=1}{\overset{\infty }{\cup }}E_n$.

Then $S$ is countable.

Proof

---

Let every set $E_n$ be arranged in a sequence $\left\{x_{\text{nk}}\right\},k=1,2,3,\text{...},$

and consider the infinite array

(16)

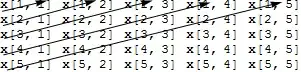
in which the elements of $E_n$ form the nth row.

The array contains all elements of $S$. As indicated by the arrows, these elements can be arranged in a sequence

(17) $x_{11};x_{21},x_{12};x_{31},x_{22},x_{13};x_{41},x_{32},x_{23},x_{14};\text{...}$

Sentence 1 If any two of the sets $E_n$ have elements in common, these will appear more than once in (17).

Sentence 2 Hence there is a subset $T$ of the set of all positive integers such that $S\sim T$, which shows that $S$ is at most countable. Since $E_1\subset S$, and $E_1$ is infinite, $S$ is infinite, and thus countable.

Problem: What's the relation between sentence 1 and sentence 2?

Answer 1

When we want to prove a set is countable, we produce an injection from said set to $\Bbb N$. Since elements may repeat in $(17)$, the author wants to avoid this to make the map actually an injection. Since here it seems countable stands for "countably infinite", the construction produces a bijection: we already have surjection since we know the sets are countably infinite to begin with, the deletion of repeated entries produces the desired bijection.

Answer 2

(17) is giving a sequence in $S$ such that every element of $S$ appears at least once as a term of the sequence. This may be viewed as a surjective function $f: \mathbb{Z}^+ \rightarrow S$. To get a bijection, starting from $1$ and working upwards we can simply remove from the domain every positive integer $n$ such that $f(n) = f(m)$ for some $m < n$. This gives a bijection: $f: T \subset \mathbb{Z}^+ \rightarrow S$.

Answer 3

It could have been stated a bit more clearly; let me expand it a bit. $(17)$ is to be understood as exhibiting this correspondence with the set of positive integers:

$$\begin{array}{rcc} \Bbb Z^+:&1&2&3&4&5&6&7&8&9&10&11&\ldots\\ S:&x_{11}&x_{21}&x_{12}&x_{31}&x_{22}&x_{13}&x_{41}&x_{32}&x_{23}&x_{14}&x_{51}&\ldots \end{array}$$

The problem is that some of the entries in the $S$ row may be identical; e.g., it might be that $x_{12}=x_{23}$ and $x_{11}=x_{22}=x_{32}$. In that case the correspondence isn’t a bijection between $\Bbb Z^+$ and $S$. However, we can strike out any duplicates in the bottom line, leaving something like this, for instance:

$$\begin{array}{rcc} T:&1&2&3&4&\bullet&6&7&\bullet&\bullet&10&11&\ldots\\ S:&x_{11}&x_{21}&x_{12}&x_{31}&\bullet&x_{13}&x_{41}&\bullet&\bullet&x_{14}&x_{51}&\ldots \end{array}$$

(I’ve replaced the deleted items with bullets for greater visual clarity; in fact the deleted items are simply gone.) We now have a bijection between the two sets that remain. On the bottom line we still have the set $S$, since we struck out only extra copies. On the top line we have some subset $T$ of $\Bbb Z^+$.

The Hence in Sentence $2$ actually refers to the fact that although we may not have a bijection of $S$ with $\Bbb Z^+$, we do have one with a subset $T$ of $\Bbb Z^+$. It’s the existence of $T$ and the fact that it may only be a subset of $\Bbb Z^+$ that follow from the previous sentence, as indicated by hence.