Zooming out a graph $f(x,y) = 0$ amounts to scaling the coordinates equally; introduce a parameter $t > 0$ and plot $f(tx, ty) = 0$. As $t\to 0$, the picture resembles zooming into the graph, while $t \to \infty$ correponds to zooming out.
In the case of $y = x^3$ or $y - x^3 = 0$, one has $(ty) - (tx)^3 = 0$ or $y = t^2x^3$. One also sees that in the case of a linear function $y = ax$, the graph looks the same at all zoom scales since the $t$ parameter cancels out.
In the example you mentioned, $y = x - \sin x$ corresponds to $ty = tx - \sin tx$ or $y = x - \frac 1t \sin tx$. Then as $t \to \infty$, the sin term drops off and the graph approaches $y = x$.
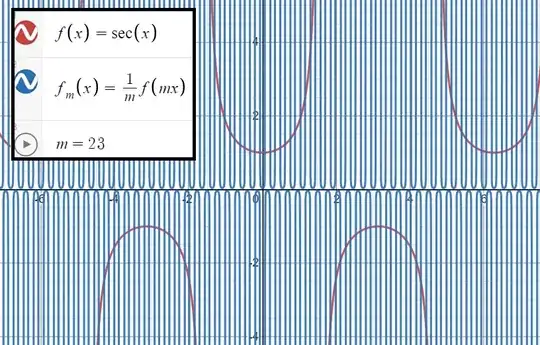
What the graph "becomes" or ultimately looks like as $t \to \infty$ can be easily described for some simple cases, like the examples above. For a more complicated example, like $y = x \sin x$, it is trickier to describe what is happening to the graph as $t \to \infty$.
For $y = x \sin x$ specifically, as you observed it resembles two large triangles, which together can be described as the set of points $T = \{(x,y) : -|x| \leq y \leq |x|\} \subset \mathbb R^2$. To argue that the graph $ty = tx \sin tx$ somehow "approaches" or "converges to" $T$ as $t \to \infty$ requires some notion of what it means for a family of subsets of $\mathbb R^2$ to "approach" or "converge to" another subset. There are many ways to interpret this idea, and some will be more useful than others in certain contexts.
My first guess to formalize this idea might go something like this: let $G_t = \{(x,y) : f(tx,ty) = 0\}$ be the graph of the desired function at the scale $t$. We will say the family of subsets $G_t$ "approaches" or "converges to" the subset $S \subset \mathbb R^2$ if it holds that $(x,y) \in S$ if and only if there is a sequence $(t_n)_n$ such that $t_n \to \infty$ as $n \to \infty$, as well as a sequence of points $(x_n,y_n) \in G_{t_n}$ such that $(x_n,y_n) \to (x,y)$ as $n\to \infty$.
With this definition, we can prove that the graph of $y = x \sin x$ approaches the two-triangles set $T$. Here is the argument:
Let $(x,y) \in T$ be arbitrary, ie $-|x| \leq y \leq |x|$ or equivalently $-1 \leq y/x \leq 1$. There is therefore a value $\theta > 0$ such that $y/x = \sin(\theta + 2\pi n)$ for all $n$, or equivalently $y = x \sin (\theta + 2\pi n)$.
So let $(t_n)_n$ be the sequence such that $t_n = \frac1x(\theta + 2\pi n)$ for each $n$ (in the case that $x \geq 0$; in the case that $x < 0$, replace $t_n$ by $-t_n$), and let $(x_n,y_n)_n$ be the constant sequence $(x,y)$. Then clearly $(x_n,y_n)_n \to (x,y)$ as $n\to \infty$, and moreover $y_n = x_n \sin (t_n x_n)$ for each $n$, ie $(x_n,y_n) \in G_{t_n}$ for each $n$.
In the converse case, suppose $(x,y) \not\in T$, ie $y/x < -1$ or $y/x > 1$. Then we want to show there is no sequence of times $t_n$ and points $(x_n,y_n) \in G_{t_n}$ such that $t_n \to \infty$ and $(x_n,y_n) \to (x,y)$ as $n \to \infty$. We can use a little topology to argue this.
Note that $G_t \subset T$ for every $t > 0$, and $T$ is a closed subset of $\mathbb R^2$. This means there can be no sequence of points from $T$ converging to $(x,y)$, if $(x,y) \not\in T$.
This completes the proof, and so we can say that the graph of $y = x\sin x$ does indeed converge to the subset $T$ of two triangles as you zoom out infinitely far (relative to the definition above).
There may be a way to interpret what I have outlined above using the idea of a limit set from the field of dynamical systems.
Coming up with some theorem about what will happen to a general graph $f(x,y) = 0$ seems like a tall order, but there are a few things you can quickly say. Any asymptotes anywhere in the domain will be pushed to the line $x = 0$. Aside from that, the picture $\lim_t G_t$ depends on the limiting behavior of $y = f(x)$ as $x \to \infty$; whether it oscillates or converges to some value or if it grows without bound. It also matters the growth rate, specifically whether it is faster or slower than a linear function.
The linear functions are (more or less) the only functions which are preserved by zooming in and out, so if $y = f(x)$ grows any faster than a linear function (all linear functions) as $x \to \infty$, this will also cause the graph to smoosh against the line $x = 0$ as $t \to \infty$. Conversely, anything which grows slower than a linear function (eg, $y = \sqrt x$ will be smooshed against the line $y = 0$ in the limit.
There is another, more compact definition for the set $S = \lim_t G_t$ if we write it in terms of the distance from a point to a set. Given a closed subset $A \subset \mathbb R^2$ and a point $(x,y) \not\in A$, we can define the distance
$$d\big((x,y), A\big) = \inf \big\{d\big((x,y), (a_1,a_2)\big) : (a_1, a_2) \in A\big\}$$
where the distance between the points $(x,y)$ and $(a_1, a_2)$ is the usual Euclidean distance formula. This says that the distance from the point $(x,y)$ to the set $A$ is whatever the smallest/minimal distance is between $(x,y)$ and any point of $A$. Using this notion, we can restate the definition of what we mean when we say the family of subsets $G_t$ converges to another subset. Namely,
$$(x,y) \in \lim_{t\to\infty} G_t \iff \lim_{t\to\infty} d\big((x,y), G_t\big) = 0$$
Using this definition, here is a proof that the graph of $y = x^2$ converges to the half-line $\{(0,y) : y \geq 0\}$ as one zooms out infinitely far.
In this case, $G_t = \{(x,y) : ty = (tx)^2\}$ or equivalently $y = tx^2$. So pick an arbitrary $y \geq 0$, in which case for each $t > 0$ one can let $x = \sqrt{y/t}$. For this $x$ and $y$ it holds that $(x,y) \in G_t$, and therefore
$$d\big((0,y), G_t\big) \leq x = \sqrt{y/t}.$$
Using the squeeze theorem, we then see that $d\big((0,y), G_t\big) \to 0$ as $t \to \infty$. This demonstrates that $\{(0,y) : y \geq 0\} \subset \lim_t G_t$. For the reverse inclusion, we would need to argue that any point $(x,y)$ with $x \neq 0$ or $y < 0$ must stay "bounded away" from the set $G_t$ for all sufficiently large $t$.
We can make use of a simple lemma: if $A_t$ is a descending family of closed subsets such that $G_t \subset A_t$ for each $t$, then $\lim_t G_t \subset \bigcap_t A_t$. This is true because, for any point $(x,y) \not\in \bigcap_t A_t$, it holds that $(x,y) \not\in A_t$ for all sufficiently large $t$ - and, because each $A_t$ is closed, any point outside of $A_t$ is a positive distance away from $A_t$.
Say, for instance, $(x,y) \not\in A_{t_0}$ and observe $G_t \subset A_t \subset A_{t_0}$ for all $t \geq t_0$. We also have, because $A_{t_0}$ is closed, that $(x,y) \not\in A_{t_0}$ implies $d\big((x,y),A_{t_0}\big) > 0$. Hence
$$d\big((x,y), G_t\big) \geq d\big((x,y), A_{t_0}\big) > 0$$
for all $t \geq t_0$, and therefore $d\big((x,y),G_t\big) \not\to 0$ as $t \to \infty$.
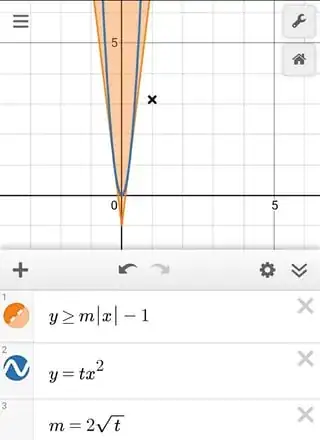
We can apply this lemma to our problem here in the following way. For each $t > 0$, let $A_t = \{(x,y) : y \geq 2\sqrt{t}|x| - 1 \text{ and } y \geq 0\}$. Observe that $(A_t)_t$ is a descending family of subsets and $G_t \subset A_t$ for each $t$. By the lemma above, we then have that
$$\lim_{t\to\infty} G_t \subset \bigcap_{t>0} A_t = \{(0,y) : y \geq 0\}$$
This completes the proof that the graph of $y = x^2$ converges to the half-line $x = 0$, $y \geq 0$ as one zooms out infinitely far. See below for an illustration of $G_t$ and $A_t$ for a particular $t$ value. The idea is that we overapproximate the graph $G_t$ by a sort of triangular cone shape (also implicitly restricting to the upper half-plane).
The reason why $\bigcap_t A_t = \{(0,y) : y \geq 0\}$ is clear from the picture; as $t \to \infty$, the slope of the boundary goes to infinity as well, and so it will "sweep past" any point $(x,y)$ with $x \neq 0$, in which case $(x,y)$ has no hope of belonging to the intersection.
There is a subtle difference between the two definitions of the set $\lim_t G_t$ that I presented above. In the first definition, $(x,y) \in \lim_t G_t$ when the set $G_t$ is close to $(x,y)$ at infinitely many times $t$, but the distance between $G_t$ and $(x,y)$ may also be large for infinitely many times. In the second definition, $(x,y) \in \lim_t G_t$ when $G_t$ is close to $(x,y)$ for all sufficiently large $t$, which is a stronger condition. This doesn't change the validity of either of the proofs I presented above, as showing convergence in the second sense will imply convergence in the first sense (but not the other way around).