The function $f(x)=\sum_{n=1}^{\infty} \frac 1 {(n + x \cdot i)^2}$

Asked Feb 05 '22 at 22:03

Active Feb 05 '22 at 22:03

Viewed 55 times

Let $f(x)$ be the complex-valued function defined by $$f(x)=\sum_{n=1}^{\infty} \frac 1 {(n + x \cdot i)^2}$$ in the real variable $x$, being $i$ the imaginary unit.

Clearly, $$f(0)=\frac {\pi^2} 6$$

Further, $$f(x)=\sum_{n=1}^{\infty} \frac {n^2-x^2} {(n^2+x^2)^2} - 2x \cdot i \sum_{n=1}^{\infty} \frac {n} {(n^2+x^2)^2}$$ therefore $$f(-x)=\overline{f(x)}$$

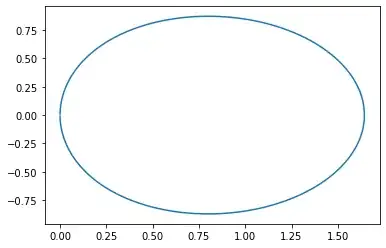
If one plots the values of $f(x)$ in the complex plane, at a first look the result is quite similar to a circle $(|x| \lt 100)$

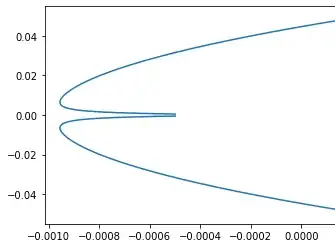
But a closer analysis shows the following behavior for large values of $|x|\;(20 \lt |x| \lt 1000)$

I ask if there are theoretical references that explain the graphs obtained.

asked Feb 05 '22 at 22:03

Augusto Santi

1,828

1

For what it’s worth, $f(x)=\psi^{(1)} (1+i x)$ where $\psi^{(1)}$ is the trigamma function. – KStarGamer Feb 05 '22 at 22:08
@KStarGamer Many thanks. – Augusto Santi Feb 05 '22 at 22:12
1

Using https://math.stackexchange.com/q/1959285/42969 you can compute $2 \operatorname{Re} f(x) = 1/x^2- \pi^2/\sinh^2(\pi x) \ge 0$. Which means that the second graph suffers from rounding errors. – Martin R Feb 05 '22 at 22:35
1

The $f$ you describe here is the well-studied Hurwitz zeta function for argument $s = 2$ and $a = 1 + i x$. About the characteristics of this precise graph, I don't know if it is studied. – aahlback Feb 05 '22 at 22:53
Can you show what precise error bounds you use? Typically one would use packages such as Nemo or Arb. – aahlback Feb 05 '22 at 23:01

The function $f(x)=\sum_{n=1}^{\infty} \frac 1 {(n + x \cdot i)^2}$

0 Answers0