1

Spivak's chapter 6, question 1 asks: for which of the following functions $f$ is there a continuous function $F$ with domain $\mathbb{R}$ such that $F(x) = f(x)$ for all $x$ in the domain of $f$. Part (iv) asks us to consider the function $f(x) = 1/q, x = p/q$ rational in lowest terms.

The answer book says: No, because it would have to be that $F(x) = 0$ for irrational $x$, but then $F$ would not be continuous at rational numbers. I understand the second part (that $F$ would not be continuous at rational $x$ if $F(x) = 0$ for irrational $x$). But I don't know how to prove the first part. If there were an $F$ such that $F(x) = f(x)$ for all $x$ in the domain of $f$, why does it follow that $F(x) = 0$ for irrational $x$?

Matthew Cassell
  • 4,248
  • 4
  • 21
  • 30
Stephen
  • 61

3 Answers3

1

The general idea is to pick some positive $\varepsilon$ and some irrational $z,$ then show that there is an open interval containing $z$ such that for every rational $x$ (in lowest terms) in that interval, the denominator is large enough that $f(x)<\varepsilon.$ Then you have to show that if $y<0,$ then there is some positive $\varepsilon$ such that no matter what $x\in\Bbb Q$ you choose, $|f(x)-y|>\varepsilon.$

Cameron Buie
  • 102,994
1

If $x$ is an irrational numbers and if $\varepsilon>0$, then, in $(x-1,x+1)$, there are only finitely many rational numbers which, when written in lowest terms as $\frac pq$, have $q\leqslant n$. So, you only have $f(y)\geqslant\frac1n$ finitely many times in $(x-1,x+1)$. Take $0<\delta<1$ such that $(x-\delta,x+\delta)$ has no element of that finite set. Then $(\forall y\in\Bbb Q):|y-x|<\delta\implies\bigl|f(y)\bigr|<\varepsilon$. This shows that $\lim_{y\to x}f(y)=0$. So, if $F$ is continuous at $x$ and if $F$ is an extension of $f$, $F(x)=0$.

José Carlos Santos
  • 427,504
0

This is roughly what the graph of $f$ looks like:

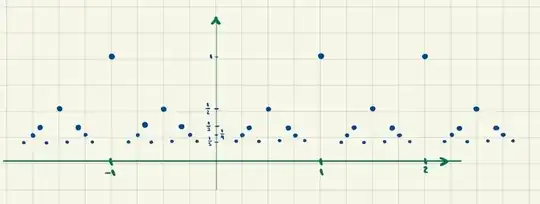
enter image description here

Note that I drew only a few blue points, representing rational values for $x$. In reality, there are infinite such points smaller than the ones I drew. They all have $f(x)>0$.

For any $a \in \mathbb{Q}$, $\nexists \lim\limits_{x \to a} f(x)$ because $f$ is not defined at irrational numbers.

That is, for any $l \in \mathbb{R}$ that we choose as a candidate for being $\lim\limits_{x \to a} f(x)$ there exists $\epsilon>0$ such that for all $\delta>0$, $\exists y$ such that it is not true that $|y-a|<\delta$ and $|f(y)-l|<\epsilon$.

The $y$ in this argument is some irrational number in the interval $|x-a|<\delta$. Since $f(y)$ is not defined, $|f(y)-l|<\epsilon$ is false.

This is the negation of the definition of this limit.

Therefore, $\lnot (\exists \lim\limits_{x \to a} f(x))$, ie $\nexists \lim\limits_{x \to a} f(x)$.

For any new function $F(x)$ such that $F(x)=f(x)$ for rational $x$, no matter how we define $F(x)$ at irrational $x$ there will be at least one (actually it will end up being infinitely many) points with rational $x$ for which $\nexists \lim\limits_{x \to a} f(x)$.

The reason why $F$ being $0$ at irrational numbers is mentioned is that this is the only choice that makes $F$ continuous at the irrational numbers. This is supposedly the "best" case scenario: continuity at irrational numbers but not at (any) rational numbers.

José Carlos Santos answer shows how we can prove continuity at the irrational $x$ with such a definition of $F$ at irrational $x$.

xoux
  • 4,913
  • It's not accurate to say that "$\lim_{x\to a}f(x)$ doesn't exist" for rational $a$ "because $f$ is not defined at irrational numbers." Consider for example the identity function on $\Bbb Q.$ It is not defined at any irrational number, and yet it is continuous, and (so) the limit exists at each point of its domain. Now, $f$ is not continuous at each point of its domain, but the limit still exists, and is equal to $0,$ at each such point. – Cameron Buie Feb 25 '22 at 01:56
  • You're saying the function $f(x) = x$, $x \in \mathbb{Q}$ is continuous (in $\mathbb{R}$)? As far as I understand, the limit $\lim\limits_{x \to a} f(x)$ doesn't exist for any $a \in \mathbb{R}$ for this function, therefore it is not continuous at any such $a$. If we slightly alter the function and make it so that it is also $0$ for $x$ irrational, then the function is only continuous at 0, but not so for any other $a$. In either case, the function is either entirely or almost entirely discontinuous. – xoux Feb 26 '22 at 04:51
  • Not at all. The identity function on $\Bbb Q$ is continuous in $\Bbb Q.$ It is neither continuous nor discontinuous at any irrational point, as it is not defined at irrational points. You're correct about the continuity of the altered function, but I wouldn't call that a "slight" alteration--you've increased the domain from countable to uncountably infinite! – Cameron Buie Feb 26 '22 at 10:46
  • To see why $\mathrm{id}{\Bbb Q}$ is continuous (in fact, uniformly continuous) on its domain, note that for any $\varepsilon>0,$ any $x\in\Bbb Q,$ and any $y\in\Bbb Q$ such that $0<|x-y|<\varepsilon,$ we have $\left|\mathrm{id}{\Bbb Q}(x)-\mathrm{id}_{\Bbb Q}(y)\right|<\varepsilon.$ – Cameron Buie Feb 26 '22 at 10:57
  • On the other hand, the function $f$ from the question is discontinuous at every point in its domain. This is because for any $\varepsilon>0$ and any $x\in\Bbb Q,$ there exists some $\delta>0$ such that whenever $y\in\Bbb Q$ and $|x-y|<\delta,$ we have $|f(y)|<\varepsilon,$ but $f(x)>0.$ – Cameron Buie Feb 26 '22 at 10:58
  • See here and here for more discussion on how to think about (dis)continuity on proper subsets of $\Bbb R.$ – Cameron Buie Feb 26 '22 at 12:13
  • Oops! I forgot to actually include the second link. – Cameron Buie Feb 26 '22 at 18:40