Proving that $S^2$ and $\bar{X}$ are independent?

Question

I came across the proof of $\frac{(n-1)S^2}{\sigma^2}\sim \chi^2_{n-1}$ here:

Proof of $\frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{n-1}$

But the respected author "Mike Spivey" has mentioned that $S^2$ and $\bar{X}$ are independent.

We have$$S^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$$

But i am really blank how to prove that they are independent? Any help or hint is appreciated.

Hint: Consider the distribution of the random vector $(\bar{Y}, Y_1 - \bar{Y},\dots, Y_n - \bar{Y})$. — user51547, Feb 03 '22 at 01:46
I'm reluctant to close this as a duplicate because the Question here does not assume a normal distribution is being sampled (see @BruceET's Comment and Answer) and because the OP is not familiar with Basu's Thm. — hardmath, Feb 04 '22 at 01:39
@hardmath That's funny because the proof OP is concerned about is in the context of a normal distribution (clear from the question https://math.stackexchange.com/questions/47009/proof-of-fracn-1s2-sigma2-sim-chi2-n-1?noredirect=1&lq=1) and one does not need to know Basu's theorem for this proof. The answers in my proposed duplicate made this clear. If this is not a duplicate then what is? — StubbornAtom, Feb 04 '22 at 06:46
@hardmath And the answer you mention here is no answer at all! — StubbornAtom, Feb 04 '22 at 06:55
@StubbornAtom: If you were to post an Answer here, making the points in your Comment and linking to the "proposed duplicate" for the normal sampling case, I'd be happy to upvote. While I understand your view, the Question here did not mention the assumption of a normal distribution, and Bruce's Answer illustrates its importance. In that sense it is a useful Answer. — hardmath, Feb 04 '22 at 07:03
@hardmath Just because the OP has not stated the normality assumption does not mean there is any confusion regarding this assumption. This is clear from the linked post in the OP. I don't see the point of me answering this question. I went through the effort of searching for an appropriate question and flagged this as an obvious duplicate of that. — StubbornAtom, Feb 04 '22 at 07:12

score 2 · Answer 1 · edited Feb 03 '22 at 23:00

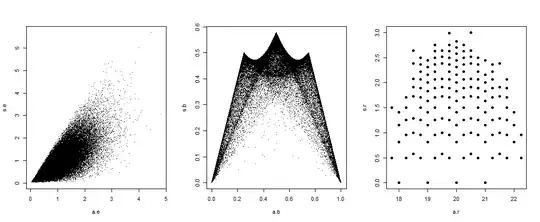
Independence of $\bar X$ and $S$ is true only for normal data. Consider standard exponential, Beta(.1, .1), and severely rounded normal data (which are no longer normal).

Plots of sample standard deviations against sample means. For exponential data, $\bar X$ and $S$ are highly correlated, for the other two cases correlation is $0,$ but plots show lack of independence.

R code for figure:

set.seed(2022)
n = 4     # sample size
m = 10^5  # data
DTA.e = matrix(rexp(m*n), nrow=m)
a.e = rowMeans(DTA.e)
s.e = apply(DTA.e, 1, sd)
DTA.b = matrix(rbeta(m*n,.1,.1), nrow=m)
a.b = rowMeans(DTA.b)
s.b = apply(DTA.b, 1, sd)
DTA.r = matrix(round(rnorm(m*n, 20)), nrow=m)
a.r = rowMeans(DTA.r)
s.r = apply(DTA.r, 1, sd)
par(mfrow=c(1,3))
 plot(a.e, s.e, pch=".")
 plot(a.b, s.b, pch=".")
 plot(a.r, s.r, pch=19)
par(mfrow=c(1,1))

Proving that $S^2$ and $\bar{X}$ are independent?

1 Answers1