2

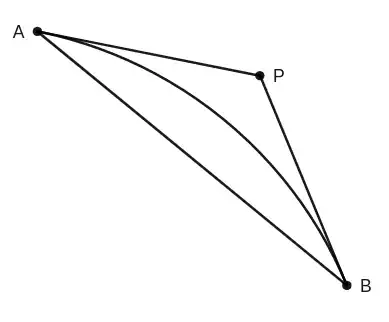
In posing part of an answer to this question, I appealed to geometry in attempting to show that $x<\tan(x)$ for $0<x<\dfrac{\pi}{2}$

Specifically, I assumed that, in the following diagram that $$AB<\overset{\mmlToken{mo}{⏜}}{AB\,}<AP+PB$$ where $A,B$ are points of tangency of lines $PA, PB$, respectively on the circular arc $\overset{\mmlToken{mo}{⏜}}{AB\,}$.

The first part of the inequality can be justified on the 'shortest distance between two points' principle. The second part of the inequality is less certain, and I was challenged on this (rightly so) by @AnshumanAgrawal.

It can be proved on the assumption that $x<\tan(x)$, but that would be circular.

The question is: Can the second part of the inequality be shown by a geometrical argument without relying explicitly or implicitly on the inequality $x<\tan(x)$?

tangents to circular arc

[Note: I'm currently battling a bad cold (not COVID) so not at my peak capacity, but I think that @AnshumanAgrawal deserves an answer to their objection. So I put this out there for those who might have some thoughts on the matter.]

John Wayland Bales
  • 21,814

2 Answers2

1

enter image description here

  1. The area of the sector of the circle delimited by the angle $A$ is : $$\dfrac{1}{2} A R^2 = \dfrac{1}{2} \text{arc}(BD) \times R$$
  2. The area of $ABPD$ is : $$\dfrac{1}{2} R \times BP + \dfrac{1}{2} R \times PD = \dfrac{1}{2} R \times (BP + PD)$$
It's clear that the area of the sector is $<$ the area of the polygon then : $$\text{arc}(BD) < BP + PD$$
Essaidi
  • 1,733
0

I think the following makes it clear and could be made into a proof.

Draw lines perpendicular to $AB$ and very close to each other.

Compare the sections of the arc and $APB$ cut off by each adjacent pair of parallel lines.