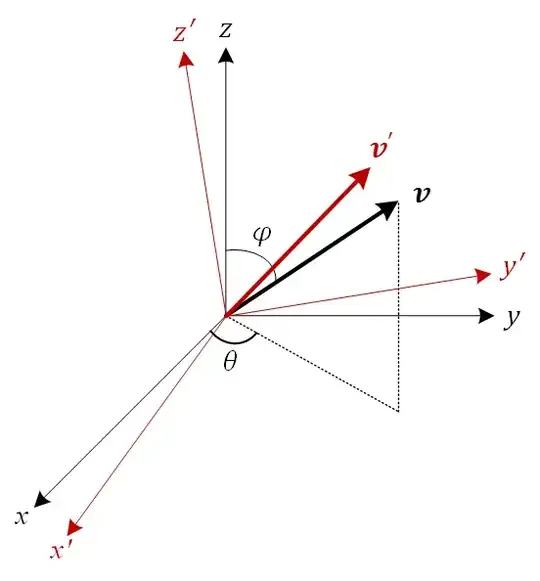
I have a reference frame $xyz$ and a vector $\mathbf{v}$ in this frame defined by the angles $\theta$ and $\varphi$ (the amplitude is not important). A rotation is performed, defined by the three Euler angles or the change in roll/pitch/yaw, which gives the frame $x'y'z'$ and the vector $\mathbf{v'}$.
Question 1: If I know only the two vectors $\mathbf{v}$ and $\mathbf{v'}$, can I determine the three angles describing the rotation performed?
From my readings (Is the rotation matrix unique for a given rotation?, $3D$ rotation matrix uniqueness, Expression of rotation matrix from two vectors), I understand that it is not possible, because there are infinite rotations that could change $\mathbf{v}$ to $\mathbf{v'}$. If you know a textbook or another source that demonstrates this I would be happy.
Question 2: Then, how many different vectors would I need to be able to determine the rotation performed? (e.g. if I have two vectors $\mathbf{v}$ and $\mathbf{w}$ that are changed to $\mathbf{v'}$ and $\mathbf{w'}$ and I know all of them, is it enough?)