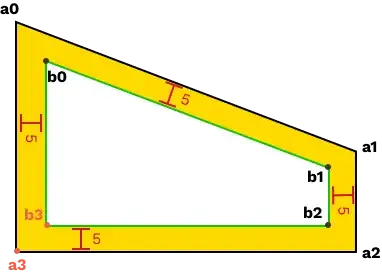
I am writing a application that needs to calculate the inner stroke of a shape. To understand more of what I mean, imagine we had a shape represented by the black outline of the image bellow. We than applied a inner stroke effect of 5 to that shape (represented by the yellow). I would now like to determine the values of points b0,b1,b2,b3. Since this application needs to be fast, I need the solution with the least amount of steps.
So far this is what I have come up with:
Intersection of parallel lines
The main solution I have thought of is getting the parallel lines of a0,a3 and a3,a2 with a distance of 5 (represented by line1 and line2). I would then calculate the intersection point of these two lines and this would determine the point b3. I would then repeat this step for the remaining points. This option requires multiple steps;
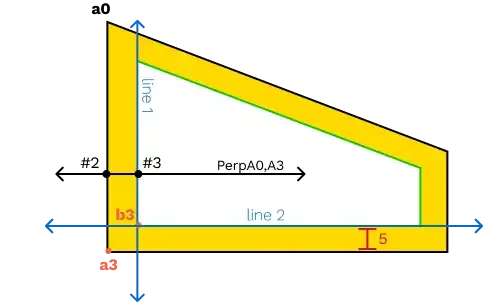
- get the perpendicular line of side a0,a3. --> PerpA0,A3
- get intersecting point of a0,a3 and PerpA0,A3 --> point #2
- use line PerpA0,A3 , point #2 and the distance of 5 to calculate point #3 example
- find the equation of the line that runs perpendicular to PerpA0,A3 and passes through point #3 giving us line1
- repeat the above steps for side a3,a2 --> line2
- calculate the point of intersection between line1 and line2 giving us point b3
I'm no math guru and don't know if this is the best solution for getting these values, If anyone could assist me I would be grateful. Also this is my first math post. Thanks.