We have to show a metric relation, which relates the length of the segment $AQ$ with a sum, and the terms of the sum are the segment $QD$ and some expression obtained by rescaling $BM$ by some factor $\lambda$. Here is a solution trying to construct related points and use as much as possible angle chasing and triangle similarities to show this relation. It is natural then to construct the segment of length $AQ-QD$, so the solution will construct a point $S$ on the segment $AQ$ to represent this length. So we will have an isolated construction in the "$D$-corner" of the picture. Then, for the rescaled version of $BM$ we also need some segment, best it should be a segment that can be easily compared with $AS$, so let us construct it having a vertex in $A$. It turns out that its construction can be best done on the line $AD$. It will be a point $N\in AD$ so that $AN$ represents this rescaled version of $BM$. So we will have a second isolated construction around the "$A$-corner" of the given parallelogram. Then it remains to relate the two constructions to each other, this is done by an equality of angles. Let's go.
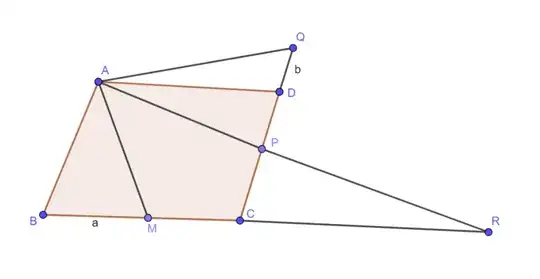
Recall the given situation, and let us introduce more notations.
Proposition:
We start with a parallelogram $ABCD$.
Pick some point $P$ on the side $CD$. We denote by $x$ the (measure of the oriented) angle $\sphericalangle PAD$. Let $Q$ be a point on the line $CPD$ so that $AQ$ is the reflection of $AP$ w.r.t. $A$, i.e. so that the (oriented) angle $\sphericalangle DAQ$ is also $x$. We denote by $y$ half of the angle $\sphericalangle BAP$, and let $M\in BC$ be the intersection of the bisector of this angle with $BC$.
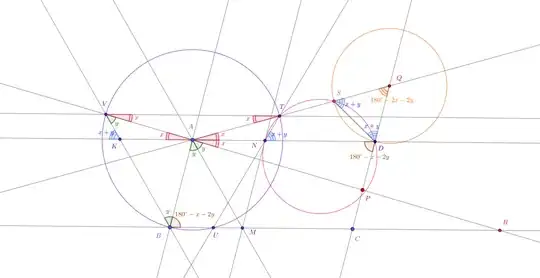
We further construct the following points:
- "In the $D$-corner" we construct a point $S$ on the segment $AQ$ so that $QS=QD$. (So $Q$ is the intersection of this segment with the circle centered in $Q$ with radius $QD$.)
- "In the $A$-corner" we construct the following many points. The parallel to $AM$ through $B$ hits $AD$ in $K$, and $AP$ in $V$. Consider a reflection w.r.t. the perpendicular in $A$ on $AD$, and draw for $B,K,V$ the respectively reflected points on the reflected lines through $A$, denoted by $U\in BC$, $N\in AD$, $T\in AQ$.
Then we have $AN=KA=BM$ and $TNDS$ is cyclic. In particular, using the power of $A$ w.r.t. the circle $(TNDS)$ we have the relation:
$$
AT\cdot AS=AN\cdot AD\ .
$$
Note: The above is equivalent to the needed relation, explicitly:
$$
AQ-b=AQ-QD=AS=\frac{AN\cdot AD}{AT}
=AN\cdot \frac{AD}{AT}
=BM\cdot \frac{AD}{AB}
=a\cdot\frac 1\lambda\ .
$$
Proof: In the "$D$-corner" we need only to compute the angle $\sphericalangle DSQ$ in terms of $x,y$. This is easy. The angle in $A$ in $ABCD$ is $x+2y$, in $D$ then $180^\circ-(x+2y)$, this angle is exterior for $\Delta ADQ$, so the angle in $Q$ in this triangle is $180^\circ -(2x+2y)$, so for the two equal angles in $S,D$ in the isosceles triangle $\Delta QSD$ remain $(x+y)$ for each one.
In "the $A$-corner", observe first that by construction $\Delta ABV$ is isosceles,
$$
\widehat{ABV}=\widehat{BAM}=y=\widehat{MAP}=\widehat{BVP}=\widehat{BVA}\ .
$$
So $B,V$ are on the same circle centered in $A$, so this is also true for the reflected points $U,T$. We have then
$\widehat{ATN}=\widehat{AVK}=y$ by reflection, so the exterior angle in $N$ in $\Delta ATN$ is the sum $x+y$ of the interior angles in $A$ and $T$.
We connect the information from the "two corners", the bridge being
$$
\widehat{TND}=x+y=\widehat{QSD}\ ,
$$
so $TNDS$ cyclic.
$\square$