Tensor with dual of locally free sheaf isomorphic to sheaf Hom

Question

During the course of trying to solve Vakil Exercise 13.1.F I decided I wanted to prove the following: Suppose $X$ is a ringed space with structure sheaf $\mathscr{O}_X$. Suppose $\mathscr{F}, \mathscr{E}$ are $\mathscr{O}_X$-modules and $\mathscr{E}$ is locally free of finite rank. Then

$$ \mathscr{F} \otimes \mathscr{E}^\vee \cong \mathcal{Hom}(\mathscr{E}, \mathscr{F}) $$

Vakil 13.7.B has us prove this in less generality, but it also mentions that the result above should hold. This should follow from the corresponding fact for modules. I couldn't find this result on the Stacks Project or elsewhere online. How do you prove it?

(I am almost certain Vakil doesn't intend 13.1.F to be solved the way I am trying to solve it given the fact that he has us prove a less general version of the result later.)

EDIT: 13.1.F becomes 14.2.F in the December 2022 version of Vakil.

Answer 1

I am going to expalin how I think of giving very formal and organised proofs for these kind of results. There are two steps:

1. Show that there exists a morphism from left to right or the other way using universal properties
2. Show that this morphism is an isomorphism on stalks or that it is an isomorphism on a covering

This "method" can be repeated on other proofs, for example if one tries to show that $\mathscr E^{\vee \, \vee} = \mathscr E$ for a locally free sheaf $\mathscr E$.

On the left you have a tensor product. Tensor products $\mathscr F \otimes \mathscr G$ are defined as sheafifications of some presheaf, which I will denote $\mathscr F \otimes_{pSh} \mathscr G$ so they are a little bit difficult to deal with. However, remember the universal property of sheafification:

$$\text{Hom}(\mathscr F^+, \mathscr G) = \text{Hom}(\mathscr F , \mathscr G)$$

which, in more down to earth words says that to give a morphism from the sheafification of a presheaf $\mathcal F$ to another sheaf $\mathcal G$ is the same as giving one from $\mathcal F$ to $\mathcal G$. Therefore, we have the task of defning a morphism $\varphi : \mathscr{F} \otimes_{psH} \mathscr{E}^\vee \to \mathcal{Hom}(\mathscr{E}, \mathscr{F})$. Note that we know the value of both presheaves on any open set (because we are now dealing with the presheaf tensor product), so we just need to define a natural $\mathcal O(U)$-linear map

$$\mathscr{F}(U) \otimes_{\mathcal O(U)} \text{Hom}_{\mathcal O_U}(\mathscr{E}_U, \mathcal O_U) \to \text{Hom}_{\mathcal O_U}(\mathscr{E}_U, \mathscr{F}_U)$$

Which is very natural:

$$ (*) \qquad s \otimes f \longmapsto \, (t \mapsto f(t) s) \in \text{Hom}_{\mathcal O_U}(\mathscr{E}_U, \mathscr{F}_U)$$

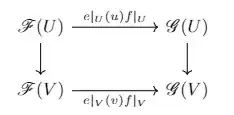
These maps clearly constitute a morphism of sheaves (they look so natural, its is clear that they commute with restrictions) and therefore putting everything together we obtain the desired morphism $\hat\varphi:\mathscr{F} \otimes \mathscr{E}^\vee \to \mathcal{Hom}(\mathscr{E}, \mathscr{F})$, corresponing to $\varphi$

Before the edit, I was going to prove that the map is an isomorphism on stalks, but one needs to prove first that $(\mathcal{Hom}(\mathscr{E}, \mathscr{F}))_p = \text{Hom}_{\mathcal O_p}(\mathscr{E}_p, \mathscr{F}_p)$ and this is not trivial. However, it is enough to show that $\varphi$ is an isomorphism on a covering of $X$. Since $\mathscr{E}$ is locally free, for the remainder of the proof it is enough to assume that $\mathscr{E}=\mathcal O_X^{\oplus n}$. In this case, we can factor $\varphi$ as

$$\mathscr{F} \otimes_{pSh} \mathscr{E} ^\vee \stackrel{\cong}{\longrightarrow} \left( \mathscr{F} \otimes_{pSh} \mathcal O_X ^\vee\right)^{\oplus n} \longrightarrow \left( \mathcal{Hom} (\mathcal O _X ,\mathscr F)\right)^{\otimes n} \stackrel{\cong}{\longrightarrow} \mathcal{Hom}(\mathscr{E}, \mathscr{F}),$$

where the left and right arrows are isomorphisms, so one reduces to the case $n=1$. In this case, the isomorphism can be checked on any open subset $V$, and using that

$$\mathcal{Hom}(\mathcal O_X , \mathscr F) (V) = \text{Hom}_{\mathcal O_X(V)}(\mathcal O_X(V) , \mathscr F (V))$$ $$\mathcal{Hom}(\mathcal O_X , \mathcal O_X) (V) = \text{Hom}_{\mathcal O_X(V)}(\mathcal O_X(V) , \mathcal O_X(V))$$

and the notation $M=\mathscr F(V)$, $R= \mathcal O_X(V)$, it is equivalent to checking that the $R$-module homomorphism

$$M \otimes_R \text{Hom}_R(R, R) \to \text{Hom}_R(R, M)$$

Given in a similar fashion as in $(*)$ is an isomorphism

Answer 2

I'm also a new learner in algebraic geometry. I'm so sorry if my understanding on this is incorrect.

Actually the dual sheaf $\mathcal{E}^{\vee}$ is the dual object in the symmetric monoidal category of $\mathcal{O}_X$-modules when $\mathcal{E}$ is locally a direct summand of a finite free $\mathcal{O}_X$-module. (See Stacks Project Tag 0FNU and 0FNV at https://stacks.math.columbia.edu/tag/0FNU) Note that this condition on $\mathcal{E}$ is more general than Vakil's one.

Then by following results on the dual object in symmetric monoidal category:

1. In symmetric monoidal categories, the left dual object and the right dual object are isomorphic. (Though I haven't found this on Stacks Project unfortunately.)
2. Tag 0FFQ of Stacks Project: https://stacks.math.columbia.edu/tag/0FFQ ,

we see that $$ \mathrm{Hom}_{\mathcal{O}_X}(\mathcal{F} \otimes_{\mathcal{O}_X} \mathcal{E}, \mathcal{G}) = \mathrm{Hom}_{\mathcal{O}_X} (\mathcal{F}, \mathcal{G} \otimes_{\mathcal{O}_X} \mathcal{E}^{\vee}). $$ Then recall the adjointness of $-\otimes_{\mathcal{O}_X} \mathcal{E}$ and $\mathcal{H}om_{\mathcal{O}_X}(\mathcal{E}, -)$, we see that $$ \mathrm{Hom}_{\mathcal{O}_X}(\mathcal{F} \otimes_{\mathcal{O}_X} \mathcal{E}, \mathcal{G})= \mathrm{Hom}_{\mathcal{O}_X}(\mathcal{F}, \mathcal{H}om_{\mathcal{O}_X}(\mathcal{E}, \mathcal{G})). $$ Comparing this two, we see that $\mathcal{G} \otimes_{\mathcal{O}_X} \mathcal{E}^{\vee} = \mathcal{H}om_{\mathcal{O}_X}(\mathcal{E}, \mathcal{G})$ by (the dual version of) Yoneda's lemma.

P.S. In the above discussions, all $=$ conneting "$\mathrm{Hom}$" should be natural isomorphisms.

Sorry for possible mistakes and misunderstandings.

Answer 3

$$ \DeclareMathOperator{\Esh}{\mathscr{E}} \DeclareMathOperator{\Fsh}{\mathscr{F}} \DeclareMathOperator{\Hom}{\mathcal{Hom}} \DeclareMathOperator{\Osh}{\mathscr{O}} $$ I believe the following should suffice. We will need the fact that $\Hom(\Esh, \Fsh)_p \cong \hom(\Esh_p, \Fsh_p)$ (for locally free finite rank $\Esh$). This follows from the fact that $\Hom$ commutes with finite direct sums and direct sums commute with taking stalks.

We begin by defining the morphism of presheaves $(\Fsh \otimes \Esh^\vee)^\text{pre} \to \Hom(\Esh, \Fsh)$. Let $U$ be an arbitrary open. Then we define $\phi_U: \Fsh(U) \otimes \Esh^\vee(U) \to \hom(\Esh|_U, \Fsh|_U)$ by sending $f \otimes e$ to the morphism of sheaves $g$ given by $g_U(x)=e_U(x)f|_U$. It is easily checked that the following diagram commutes:

Hence we have defined the desired morphism. By universal property of sheafification, we get a morphism $\Fsh \otimes \Esh^\vee \to \Hom(\Esh, \Fsh)$. Now, since $\Esh$ is finite locally free, we may localize at $p$ to check isomorphism. This gives us a morphism of modules $\Fsh_p \otimes \Esh^\vee_p \to \hom(\Osh_{X,p}^n, \Fsh_p)$ such that $f \otimes e \mapsto e(x)f$. By general module theory, this is an isomorphism, hence we have the desired global isomorphism.