2

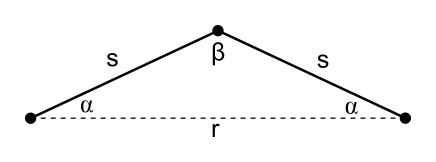
I'm trying to solve how much "bend" (angles $\alpha$ and $\beta$) a chain of $N$ equal sized (s) links so that the end to end straight line distance $(r)$ is a given value. I chose to look at this with my high school geometry skills. If it's 2 links, it's easy:

please

Law of Sines/Cosines makes it easy.

A four bar mechanism wouldn't be solvable, except for my constraints that all links are the same length, and they interior angle is uniform from link to link.

enter

Introducing $d$, noting that $2\alpha + 2\beta = 2\pi$, I could come up with a couple equations, substitute a bunch an come up with:

$$\beta = \cos^{-1}\left(\frac{s² - r²}{2s(s + r)}\right)$$

Works like a charm. Hoping that if I could make it through a 5 sided beast, I'd see a general pattern, I had a go at it.

image-description

I came up with the following five equations (and five unknowns) to try:

\begin{align} &2\alpha + 3\beta = 3\pi\\ &\beta= \pi - 2\alpha_1\\ &\alpha= \alpha_1 + \alpha_2\\ &d^2= s^2 + s^2 - 2ss\cos\beta\\ &s^2 = s^2 + d^2 - 2ds\cos\alpha_1\\ \end{align}

(where $\alpha_1$ and $\alpha_2$ are $\alpha$ subdivided to either side of $d$)

I tried to crunch this all, but got to points where it wasn't clear how to isolate it any better.

Which caused me to pause and wonder if I was trying too hard and there was a simpler more direct way to see the solution to the problem.

I'm fine if the answer is "go back and try again to solve your 5 equations, you must've made a mistake". But I was looking for some reassurances that is the right way to go, and that I'll start to see a general pattern that generalizes for $N$ links.

(As a programmer, I could just do a convergent iteration on $\beta$ to hone in on the value that produces $r$, but I was trying to do this generally).

ACB
  • 3,713
Travis Griggs
  • 131
  • 3
  • For $n$ links $2\alpha+(n-1)\beta=(n-1)\pi$ and you get an equation for the lengths along the $r$ axis involving a sum of cosines of angles in an arithmetic progression, see this for example. – dxiv Jan 27 '22 at 00:01

1 Answers1

1

The links of length $s$ and the line of length $r$ are chords of a circle through the points where links meet. Let $2\theta $ be the angle subtended by a link at the centre of the circle. The line of length $r$ then subtends an angle of $N\theta$. Note that $\pi = \beta +2\theta.$

Basic geometry then gives the only equation that is needed

$$\frac{ \sin (N\theta)}{\sin \theta}=\frac{r}{s}.$$

For given values of $N,r,s$ this equation can be solved numerically giving the value of $\theta$ and hence the values of $\beta$ and $\alpha$. (An algebraic method can be used for small $N$.)

N.B. The above formula assumes that the centre of the circle is 'below' the chord of length $r$. If it is above that line then $N\theta $ can be replaced by $\pi - N\theta $ in the formula.

Please ask if anything is unclear in this brief description.