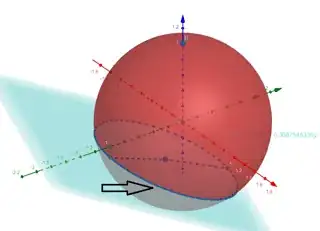
I am trying to determine the fraction of the day an observer on Earth receives sunlight as a function of the time of the year and latitude. For that, consider the circle formed by the intersection of a plane and a sphere, which are given by the following equations: $$x \cos(w) \sin(\delta)+y \sin(w)\sin(\delta)+z \cos(\delta)=\sin(L)$$ $$x^2+y^2+z^2=1$$ The part of such circle within $x>0$ is the region that receives sunlight. Therefore, I need to calculate the arc length of the circle for $x>0$ or the angle subtended by the arc for $x>0$, but I do not know how to progress further.
I have tried to determine the subtended angle using the distance between the two intersection points of the circle with the $x=0$ plane, but that does not work for every value of $L$ or $w$. I also thought about parametrizing the circle and using the arc length formula, but it is not clear for me how to do that.
For those who are interested, the circle above can be interpreted as the path of the observer throughout the day, and the positive $x$ direction points to the sun. $w$ is equal to $\omega t$, that is, the angular velocity of the Earth around the Sun times $t$, the elapsed time since a solstice.