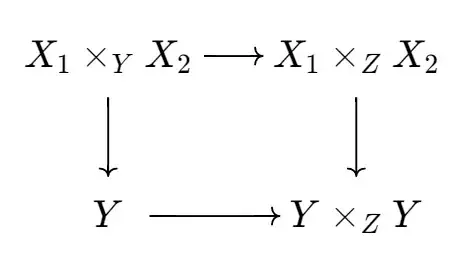Where does the map $X_1\times_ZX_2\rightarrow Y\times_ZY$ come from in the Magic Diagram? Why is it commutative?

Question

Given a morphism $Y\rightarrow Z$ and morphisms $X_1\rightarrow Y$, $X_2\rightarrow Y$, the magic diagram is given by the diagram

The question I have is about the map on the right. There are three different maps that could refer to, as far as I can tell. Consider the following diagram:

The maps $Y\rightarrow Y$ are the identity maps. The issue I'm having is that this diagram is not commutative: there is no reason the $X_1\times_ZX_2\rightarrow X_i\rightarrow Y$ for $i=1,2$ should agree. Indeed, suppose we are in $\mathsf{Set}$ and the $X_i$ and $Z$ are singletons and $Y$ is a two-element set, where the maps $X_i\rightarrow Y$ pick out different elements of $Y$. Then $X_1\times_ZX_2$ is a singleton, so the maps $X_1\times_ZX_2\rightarrow X_i\rightarrow Y$ do not agree - in general all we know is that they do agree once compose with $Y\rightarrow Z$.

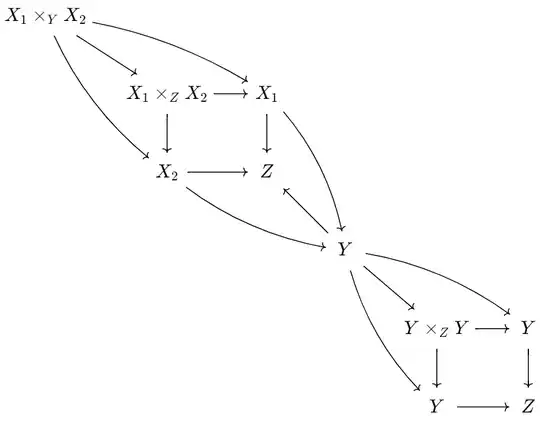
So there are two possible maps $X_1\times_ZX_2\rightarrow Y\times_ZY$, given by $X_1\times_ZX_2\rightarrow X_i\rightarrow Y\rightarrow Y\times_ZY$, as in the diagram. And these definitely aren't equal in general, for if they were, knowing $Y\rightarrow Y\times_ZY\rightarrow Y=\text{id}_Y$, we would then be able to conclude the $X_1\times_ZX_2\rightarrow X_i\rightarrow Y$ are equal.

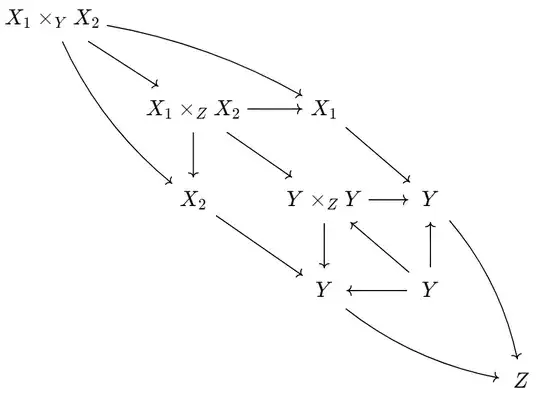
I have seen this answer, but I think the same issue arises (in fact I based that diagram off the one in the answer), that there are two maps from $X_1\times_ZX_2$ we could use. Even if we ignore this and just choose one of them, while commutativity of the magic diagram becomes easy to show, I'm not sure about the universal property. For example, suppose we have the following diagram:

These maps are given such that the red and blue paths are equal after composing with $Y\rightarrow Y\times_ZY$, which means they must actually be equal (seen by then composing with $Y\times_ZY\rightarrow Y$ since the arrows $Y\rightarrow Y$ are the identity). But I don't see why the blue map should be equal to $A\rightarrow X_1\times_ZX_2\rightarrow X_2\rightarrow Y$, just because they are equal after composing with $Y\rightarrow Z$. As a result I'm not sure how to get two maps $A\rightarrow X_i$, equal after going to $Y$, which would give me the desired $A\rightarrow X_1\times_YX_2$.

There is a third possibility for the map $X_1\times_ZX_2\rightarrow Y\times_ZY$, using the universal property of $Y\times_ZY$. This comes from the two not-necessarily-equal maps just mentioned from $X_1\times_ZX_2$ to $Y$. Since these are equal after composing with $Y\rightarrow Z$, they must each factor through $Y\times_ZY$, as in the following diagram:

If the map $X_1\times_ZX_2\rightarrow Y\times_ZY$ came from this diagram, I don't know how to show the magic diagram is commutative, although it is easy to show that if it is, then it's also a pullback.

I'm wondering whether my reasoning so far is correct. I rather suspect my "universal property morphism" is the correct morphism and not the ones which go through the $X_i$ but I don't know how to then finish the problem.

Answer 1

I think the third option is the correct one: the two maps $X_1 \times_Z X_2 \to X_i \to Y$ agree over $Z$, so the unviersal property gives us a map $X_1 \times_Z X_2 \to Y \times_Z Y$.

Before we start with the second part, let me state a small convention, which is useful when denoting morphisms with fibered products. Imagine that we have some maps $\alpha_i\colon A_i \to B$ for $i=1, 2$, and the fibered product $A_1 \times_B A_2$. Given $\beta_i\colon C \to A_i$ such that $\alpha_1 \circ \beta_1 = \alpha_2 \circ \beta_2$ (as maps $C \to B$), the universal property gives us a unique map $\phi\colon C \to A_1 \times_B A_2$. We will denote $\phi=(\beta_1, \beta_2)$, to highlight the fact that $\phi$ is induced by this pair of maps. (It will be useful for later to note that $\pi_i \circ (\beta_1, \beta_2)=\beta_i$, i.e. that $\pi_i\colon A_1 \times_B A_2 \to A_i$ recovers the correct component.)

That is the key idea with fibered products: maps $\phi\colon C \to A_1 \times_B A_2$ are in bijective correspondence with pairs of maps $\alpha_i\colon C \to A_i$, compatible "over $B$". As a nice exercise to see if this makes sense, you can check that if $\gamma\colon D \to C$ is anoter morphism, then $\alpha_i \circ \gamma\colon D \to A_i$ induce the map $\phi\circ \gamma$. This is, $(\beta_1, \beta_2) \circ \gamma=(\beta_1 \circ \gamma, \beta_2 \circ \gamma)$.

Let's get back to the problem. Let $f_i\colon X_i \to Y$ and $g\colon Y \to Z$. The bottom map of the diagram is the "diagonal map" $(id_Y, id_Y)\colon Y \to Y \times_Z Y$. The right one is $(f_1 \circ \pi_1, f_1 \circ \pi_2)$, where $\pi_i\colon X_1 \times_Z X_2 \to X_i$ are the projections. (In fact, we have that $$ g \circ (f_1 \circ \pi_1)=(g \circ f_1) \circ \pi_1 = (g \circ f_2) \circ \pi_2 = g \circ (f_2 \circ \pi_2), $$ where the second equality comes from the commutative diagram that defines $X_1 \times_Z X_2$.

The top arrow is $(\tau_1, \tau_2)\colon X_1 \times_Y X_2 \to X_1 \times_Z X_2$, where $\tau_i\colon X_1 \times_Y X_2 \to X_i$ are the projections. The compatibility condition that we have to check for this map is $(g \circ f_1)\circ \tau_1=(g \circ f_2) \circ \tau_2$, which follows from the fact that $f_1 \circ \tau_1 = f_2 \circ \tau_2$ (the commutativity of the diagram that defines $X_1 \times_Y X_2$.

At last, the left arrow is $f_1 \circ \tau_1 = f_2 \circ \tau_2 \colon X_1 \times_Y X_2 \to Y$.

We are ready to start taking compositions. The bottom-left composition is $$ (id_Y, id_Y) \circ (f_1 \circ \tau_1)=(f_1 \circ \tau_1, f_1 \circ \tau_1)=(f_1\circ \tau_1, f_2 \circ \tau_2). $$ The top-right is $$ (f_1 \circ \pi_1, f_2 \circ \pi_2) \circ (\tau_1, \tau_2). $$ To compute this composition, we have to ask ourselves, what are the maps to each coordinate? To the first one is $$ f_1 \circ \pi_1 \circ (\tau_1, \tau_2) = f_1 \circ \tau_1. $$ This is because, as we mentioned above, the pair $(\alpha_1, \alpha_2)$ "codifies" the maps to each component, and so composing with $\pi_i$ recovers $\alpha_i$. The second map is $$ f_2 \circ \pi_2 \circ (\tau_1, \tau_2) = f_2 \circ \tau_2. $$ Therefore, the top-right composition is $(f_1 \circ \tau_1, f_2 \circ \tau_2)$, and so it agrees with the left-bottom.