7

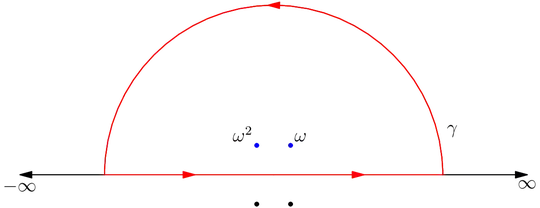
If $\int_{0}^{\infty}\frac{dx}{1+x^2+x^4}=\frac{\pi \sqrt{n}}{2n}$, then $n=$

$\text{A) }1 \space \space \space \space \space\text{B) }2 \space \space \space \space \space\text{C) }3 \space \space \space \space \space\text{D) }4 \space \space \space \space \space\text{E) }\text{None of the given options}$

Using partial fraction decomposition, I ended with $n=3$, that is option $\text{C}$. However, it took me about $8$ minutes, which is not feasible for an MCQ test, where the average time to solve a problem is $3$ minutes, and no calculator is allowed.

I believe that there is something obvious for some of you. If there is nothing obvious, then there must be a simpler and a quicker way than partial fraction decomposition.

This post is voted to be closed and considered as [duplicate] but it is not. To prove is different than evaluating $n$ with possibly a cliver and a fast way. To prove, I can use partial fraction decomposition. Some users DO NOT really read the post properly!

Please share your thoughts. THANKS!

Hussain-Alqatari
  • 5,065
  • 2
  • 13
  • 39
  • 13
    @markvs $\frac{\pi}{2\sqrt{3}}$ is approximately $0.906...$ which is the probability that you did not read my post properly. – Hussain-Alqatari Jan 22 '22 at 18:55
  • I don't think there is a faster method. Aside from bounding it between two values, but since E is an option (assuming that they haven't told you $n \in \mathbb N$) I think you're stuck with partial fractions... – Gregory Jan 22 '22 at 19:05
  • If you're familiar with complex analysis, this can be solved quickly by contour integration. The roots of $f(x) = x^4 + x^2 + 1$ in the upper-half plane are $\alpha, \beta = \pm \frac{1}{2} + i \frac{\sqrt{3}}{2}$, so $2 \int_{0}^{\infty}{\frac{1}{f} , dx} = 2 \pi i (\frac{1}{f'(\alpha)} + \frac{1}{f'(\beta)}) = \frac{\pi}{\sqrt{3}}$. In fact you probably don't have to do the arithmetic as you can be sure the answer can only involve $\sqrt{3}$. – Ant Jan 22 '22 at 19:17
  • 3
    Does this answer your question? Prove that $\int_{-\infty}^{+\infty} \frac{1}{x^4+x^2+1}dx = \frac{\pi}{\sqrt{3}}$ – okzoomer Jan 22 '22 at 19:17
  • Also have a look there: https://en.wikipedia.org/wiki/Glasser%27s_master_theorem – DavidP Jan 22 '22 at 19:21

3 Answers3

11

Note that $I=\int_{0}^{\infty}\frac{1}{1+x^2+x^4}dx\overset{x\to \frac1x}= \int_{0}^{\infty}\frac{x^2}{1+x^2+x^4}dx $. Then $$I= \frac12\int_{0}^{\infty}\frac{1+x^2}{1+x^2+x^4}dx= \frac12\int_{0}^{\infty}\frac{d(x-\frac1{x})}{(x-\frac1{x})^2+3}dx\overset{t=x-\frac1x}=\frac\pi{2\sqrt3} $$

Quanto
  • 97,352
  • I was compiling the answer but you beat me to it ;( – DatBoi Jan 22 '22 at 19:15
  • 1
    In case anyone's lost, this uses Glasser's master theorem. – J.G. Jan 22 '22 at 19:27
  • 5
    @J.G. to be more technical this doesn't use Glasser master theorem but the proof of the theorem, since the full conditions are not applicable (the bounds, etc). Instead the answer goes around the theorem by exploiting symmetry to get the integral in terms of $f(u) du$. But I love any reference to Glasser master theorem. – Ninad Munshi Jan 22 '22 at 19:48
  • 1
    @NinadMunshi The bounds are appropriate, but there was a typo twice that hid that, so I've edited accordingly. – J.G. Jan 22 '22 at 19:54
  • It looks like an easy job. So I voted up already. But still trying to understand this substitution. First time I see such things. Kindly provide me a link or the name of a text book to refer. Thank you. – Hussain-Alqatari Jan 23 '22 at 15:44
  • @Hussain-Alqatari - The substitution $t=x-\frac1x$ is just a clever trick (less-known maybe) that converts the integrand $\frac{1+x^2}{1+x^2+x^4}$ to the familiar form $\frac{1}{t^2+3}$. I don’t think there is anything profound. – Quanto Jan 23 '22 at 16:23
  • @Quanto If $t=x-\frac{1}{x}$, then $dt=(1+\frac{1}{x^2})dx$, then we need to solve for $dx$ in terms of $t$. Can you please help? – Hussain-Alqatari Jan 23 '22 at 17:58
  • @Hussain-Alqatari - Note that $$\frac{(1+x^2)dx}{1+x^2+x^4}= \frac{(1+\frac1{x^2})dx}{1+\frac1{x^2}+x^2}=\frac{dt}{3+(\frac1{x}-x)^2}= \frac{dt}{3+t^2}$$ – Quanto Jan 23 '22 at 18:11
4

There's a very quick way to do it with complex analysis:
Consider the semicircular contour integral $$\int_{\gamma} \frac{dz}{1 + z^2 + z^4}$$ Example contour to integrate along around the poles $\omega = e^{i\pi / 3}$ and $\omega^2 = e^{2i\pi / 3}$. As the radius of the semicircle increases, the integral along the curved part decreases in magnitude, and the integral approaches $$\int_{-\infty}^\infty \frac{dx}{1 + x^2 + x^4},$$ twice our desired integral. By Cauchy's residue theorem, this will be $2\pi i$ times the sum of the residues at $\omega$ and $\omega^2$. By L'Hospital's rule, the residue at $\omega$ is $$\lim_{z \to \omega} \frac{z - \omega}{1 + z^2 + z^4}dz = \lim_{z \to \omega}\frac{1}{2z + 4z^3} = \frac{1}{\sqrt3i - 3} = -\frac{\sqrt3 i + 3}{12}.$$ Similarly, the residue at $\omega^2$ is $$-\frac{\sqrt3 i - 3}{12}.$$ Thus, $$\int_{-\infty}^\infty \frac{dx}{1 + x^2 + x^4} = 2\pi i\left(-\frac{\sqrt3 i + 3}{12} + -\frac{\sqrt3 i - 3}{12}\right) = \frac{\pi\sqrt3}{3}.$$ This means the desired integral equals $\pi \sqrt3 / 6$, so the answer is $\boxed 3$.

Joseph Camacho
  • 1,617
4

$$ \begin{aligned} \int_{0}^{\infty} \frac{1}{1+x^{2}+x^{4}} d x &=\int_{0}^{\infty} \frac{\frac{1}{x^{2}}}{x^{2}+\frac{1}{x^{2}}+1} d x \\ &=\frac{1}{2} \int_{0}^{\infty} \frac{\left(1+\frac{1}{x^{2}}\right)-\left(1-\frac{1}{x^{2}}\right)}{x^{2}+\frac{1}{x^{2}}+1} d x \\ &=\frac{1}{2}\left[\int_{0}^{\infty} \frac{d\left(x-\frac{1}{x}\right)}{\left(x-\frac{1}{x}\right)^{2}+3}-\int_{0}^{\infty} \frac{d\left(x+\frac{1}{x}\right)}{\left(x+\frac{1}{x}\right)^{2}-1}\right] \\ &=\frac{1}{2}\left[\frac{1}{\sqrt{3}} \tan ^{-1}\left(\frac{x-\frac{1}{x}}{\sqrt{3}}\right)-\frac{1}{2} \ln \left|\frac{x+\frac{1}{x}-1}{x+\frac{1}{x}+1}\right|\right]_{0}^{\infty} \\ &=\frac{1}{2}\left[\frac{1}{\sqrt{3}}\left(\frac{\pi}{2}-\left(-\frac{\pi}{2}\right)\right)\right] \\ &=\frac{\pi \sqrt{3}}{6} \end{aligned} $$

Hence the answer is

$$\boxed{C) :n=3.}$$

Lai
  • 20,421