2

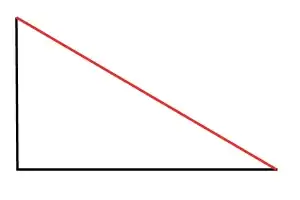
We all know that $a^2+b^2=c^2$ in a right-angled triangle, and therefore, that $c<a+b$, so that walking along the red line would be shorter than using the two black lines to get from top left to bottom right in the following graphic:

Now, let's assume that the direct way using the red line is blocked, but instead, we can use the green way in the following picture:

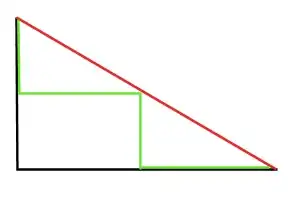
Obviously, the green way isn't any shorter than the black one, it's just $a/2+b/2+a/2+b/2 = a+b$. Now, we can divide the green path again, just like the black path, and get to the purple path. Dividing this one in two halfs again, we get the yellow path:

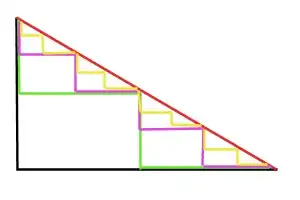
Now obviously, the yellow path is still as long as the black path from the beginning, it's just $8*a/8+8*b/8=a+b$. But if we do this segmentation again and again, we approximate the red line - without making the way any shorter. Why is this so?

egreg
  • 238,574
vauge
  • 323
  • 2
    http://math.stackexchange.com/questions/12906/is-value-of-pi-4 – Inquest Jul 04 '13 at 17:59
  • A simple reason: From basic Euclidean geometry we can prove Pythagoras Theorem. So we know a^2+b^2=c^2. Your question is equivalent to asking, why doesn't a+b=c, given a^2+b^2=c^2? Well, they are not equal because, for example, 3^2+4^2=5^2, yet 3+4 does not =5 (so we found a counterexample). In reality, you are asking why a sub i + b sub i does not equal c sub i. If any did, then adding all the as and bs and cs together on respective side of equations would result in a+b=c (which we know is false), since i is arbitrary, ai+bi=ci can't hold for some but not others, so it holds for none. – Jose_X Oct 30 '16 at 12:27

1 Answers1

4

Essentially, it is because the distance of the stepped curve from the line does not get small compared to the length of the steps.

An example where the limit is properly found is dividing a circle into $n$ equal parts and computing the sum of the line segments connecting the endpoints of the arcs. This $does$ converge to the length of the circle because the height of each arc gets arbitrarily small compared to the length of each arc as $n$ gets large.

marty cohen
  • 107,799
  • http://math.stackexchange.com/questions/12906/is-value-of-pi-4/1933209#1933209 shows this effect I think. Although the reasoning there is not that the arc "height" gets arbitrarily close but rather that the arc approximates a line and that line's length is approximated arbitrarily close by the sum of the two pieces that mark off that arc. The two pieces are each 1/2 of adjacent sides in a circumscribed regular polygon (or number of sides approaching infinity). – Jose_X Sep 25 '16 at 22:14
  • I redid the argument to use inscribed polygon, much like what you depict (rather than circumscribed as done earlier but gave incorrect link). Then made a gif that tries to show the effect simply http://math.stackexchange.com/a/1991404/10963 . [btw, I meant to post the following link in the prior comment http://math.stackexchange.com/a/1933209/10963 ] – Jose_X Oct 30 '16 at 12:33
  • the height of each arc gets arbitrarily small compared to the length of each arc as n gets large.* Could you elaborate on this? Why does the height getting small relative to the length matter or help here?
    • – user182601 Feb 01 '24 at 09:08