5

Recently, I keep coming across terms containing "Lipschitz" pertaining to statistical models and machine learning. This includes terms such as "p-lipschitz (rho), lipschitz convexity, lipschitz loss, lipschitz continuity, lipschitz condition, etc.

For example, the (famous) Gradient Descent algorithm that is used heavily in the field of machine learning to optimize the "loss functions" of Neural Networks, allegedly claims that it can provide a solution arbitrarily close to the true solution, provided an infinite number of iterations and that the "loss function" is "Lipschitz Continuous":

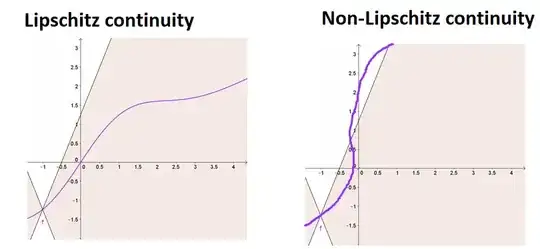
enter image description here

Although the mathematical definitions of the Lipschitz Condition are quite detailed and complicated, I think I was able to find a simple enough definition to understand for this question:

enter image description here

I am not sure if this is correct or not, but from an applied perspective : I have heard that the Lipschitz Condition is a desirable property for mathematical functions (and the gradients of these functions) because it suggests that "small changes in the input values of the function can not result in infinite values of the output of the same function".

My intuition is that if a function you are dealing with does not satisfy the Lipschitz Condition and can potentially grow in infinite size provided small changes in the inputs - this would suggest that this function has the ability to display very volatile, erratic and chaotic behaviors, making it fundamentally difficult unpredictable and unstable to deal with:

enter image description here

My Question: When it comes to complicated mathematical functions (e.g. functions that model natural phenomena in the real world), we can use the definitions of "convexity" (e.g. provided here) to find out if the function is convex or non-convex (i.e. if the function does not follow the required convexity conditions, it must be non-convex).

Can the same be said about real world functions obeying the Lipschitz Condition?

For example - if we look at the specific "loss function" being used in a specific neural network (e.g. specified number of layers, neurons, types of activation function, etc.), it might be possible to prove whether this "loss function" obeys the Lipschitz Condition.

But what about the original function that we are trying to approximate with the neural network itself?

At this point, are we just assuming that natural phenomena in the real world (e.g. ocean tides, economic patterns in the market, animal migration trajectories, etc.) are obeying the Lipschitz Condition - either in their su generis form, or for the sake of the machine learning algorithms to work?

Thanks!

almosteverywhere
  • 2,080
stats_noob
  • 3,112
  • 4
  • 10
  • 36
  • 1
    I think this is a great question, but I think it is more suited for https://physics.stackexchange.com/. You're asking about the physical systems that we use mathematics to model, and the underlying assumptions about these physical systems. – Matt E. Jan 15 '22 at 18:42
  • Just a movement $x(t)$ of an object with respect to time $[0, T]$. This is continuously differentiable w.r.t. time and hence Lipschitz continuous. So there is a lot - especially if you look at scenarios in which time is bounded. – Hyperbolic PDE friend Jan 15 '22 at 18:57
  • @Meowdog Continuously differentiable is equivalent to Lipschitz? I've never heard that one before – FShrike Jan 15 '22 at 19:08
  • 1
    Continuously differentiable on a compact domain, yes. Is a consequence from the fundamental theorem of calculus. But let me be precise: It is not equivalent. The implication is "$C^1$ on compact domain $\implies$ Lipschitz" – Hyperbolic PDE friend Jan 15 '22 at 19:10
  • Move the main question to the very top and then provide the motivation. The point of your question should be graspable within seconds. – Rodrigo de Azevedo Jan 15 '22 at 19:19
  • 1
    See the comments and answers to the recent mathoverflow question Reference request: importance of Lipschitz continuity. For example, Lipschitz continuity is simply the condition that the set of all (average) rates of change is bounded (a "rate of change" analogy to the requirement that the set of all values of a function is bounded), this assumption being made without any requirement that any of the limits of rates of change (i.e. derivative) exist, although this is the case at many points anyway. – Dave L. Renfro Jan 15 '22 at 19:28
  • A good question to ask. Practically one tries stuff in the 'real world' without verifying all the conditions. But to actually prove stuff one needs to add assumptions. Generally real world things are smooth to some extent, lack of smoothness tends to come when 'infinite processes' are involved (a bit informal, sorry). The Lipschitz condition is fairly mild (the max rate of change is limited) and has useful properties (function is differentiable ae, for example). – copper.hat Jan 15 '22 at 19:43
  • Also, and a biggie, any convex function defined on an open set is locally Lipschitz. – copper.hat Jan 15 '22 at 19:48
  • Asking whether something can be done "in the real world" is a bit of misplaced concern. The demonstration of convexity requires (at least potentially) the ability to evaluate a function, and the same is true of the Lipschitz continuity property. Machine learning is an especial focus of sister site Cross Validated and a search there for "lipschitz loss function" returns more than a dozen hits. – hardmath Jan 20 '22 at 01:21

1 Answers1

2

One condition where Lipschitz continuity naturally arises is if the function is differentiable with a bounded derivative. Let's say the function $f$ is continuous on $[a,b]$, differentiable on $(a,b)$ and the derivative is bounded: $\left|\frac{df}{dx}\right|\le M$. As per Mean Value Theorem:

$$f(b)-f(a)=\frac{df}{dx}(\xi)(b-a)$$

for some $\xi\in(a,b)$. Now, applying modulus and using the above condition of boundedness, we get:

$$|f(b)-f(a)|=\left|\frac{df}{dx}(\xi)\right||b-a|\le M|b-a|$$

Notice if the condition is satisfied on the whole $[a,b]$, then it is satisfied on any subinterval $[x,y]\subset [a,b]$ for the same $M$, so:

$$|f(y)-f(x)|\le M|y-x|$$

for all $x,y\in[a,b]$, which is the Lipschitz condition.

One special case of this is of the function $f$ that is continuously differentiable on $[a,b]$ because, well, $\frac{df}{dx}$ is then continuous and thus necessarily bounded.

If you can now argue that, in most applications of calculus in physics and natural sciences, all real functions of a real variable are not only continuously differentiable once, but are normally continuously differentiable infinitely many times, in fact they are analytic - then they will all be Lipschitz functions on any closed finite interval due to the previous statement.

  • In your last sentence "finite interval" should be "compact interval". Or change the conclusion to "... be locally Lipschitz due to ...". – Dave L. Renfro Jan 15 '22 at 20:26
  • @DaveL.Renfro Point taken, though I don't want to make this more complicated to read. May just call it "finite closed interval" and sneak somewhere that the domain is meant to be a subset of $\mathbb R^n/\mathbb C^n$... or maybe just park it at real functions of one variable and see if the OP is happy with the answer... –  Jan 15 '22 at 20:30
  • Also, in a certain sense the notion of Lipschitz continuity is more elementary and basic than that of continuous differentiability, since the latter involves the introduction of and existence of limits, whereas the former is simply a bound on "slope computations", in the same way that the notion of a function increasing on an interval is more elementary and basic than that of a function having a positive derivative on that interval. Here I'm talking about the notion (i.e. the concept) itself, and not about how to verify it for certain specific types of explicitly defined functions. – Dave L. Renfro Jan 15 '22 at 20:34