Could we build a truth table of "$P \Rightarrow \lnot P$"? What is its meaning and its Venn Diagram?

Question

The usual truth table of $P \Rightarrow Q$ looks like this

$P$	$Q$	$P \Rightarrow Q$
True	True	True
True	False	False
False	True	True
False	False	True

Before determine the truth or false of $P \Rightarrow Q$.

$P \Rightarrow Q$ is like a claim.

And when we are sure that there is no way to have a condition where

$P$ is true and $Q$ is false.

Until now the claim is considered true.

Is an implication of the form $P \Rightarrow \lnot P$ valid or not valid?

What I mean by "valid" is from the quote in a book "How to prove it by D.J. Vellman".

We will say that an argument is valid if the premises cannot all be true without the conlcusion being true ads well.

At a guess, does the truth table look like this?

$P$	$\lnot P$	$P \Rightarrow \lnot P$
True	False	False
False	True	True

But what is its meaning and venn diagram?

There's a venn diagram by hand.

https://i.stack.imgur.com/NHfyS.jpg

Answer 1

Personally I like to think of $P \to Q$ as a "promise" or "contract":

I promise if $P$, then $Q$

So if I say:

I promise if "bob dies", then "I pay \$100"

• If bob dies ($P=T$), and don't pay \$100 ($Q=F$), I've broken my promise ($F$).
• If bob dies ($P=T$), and I pay \$100 ($Q=T$), I've kept my promise ($T$).
• If bob is alive ($P=F$), and I pay \$100 ($Q=F$), I've kept my promise ($T$).
  • Just because I paid you \$100, doesn't mean bobs dead.
• If bob is alive ($P=F$), and I don't pay \$100 ($Q=F$), I've kept my promise ($T$).

For $\lnot P \to P$

Your statement $\lnot P \to P$ can be interpreted as:

I promise if "I haven't paid \$100", then "I've paid \$100"

• If haven't paid \$100 ($P=F$), then I've broken the promise ($\lnot P \to P = F$).
• If I've paid \$100 ($P=T$), then I've kept the promise ($\lnot P \to P = T$)

From this we can deduce, the promise is broken only when I don't pay \$100. Or in other words it's all based on whether I've paid \$100 ($P$). Symbolically: $\lnot P \to P = P$

For $P \to \lnot P$

The statement $P \to \lnot P$ can be interpreted as:

I promise if "I have paid \$100", then "I haven't paid \$100"

• If haven't paid \$100 ($P=F$), then I've kept the promise ($\lnot P \to P = T$).
• If I've paid \$100 ($P=T$), then I've broken the promise ($\lnot P \to P = F$)

From this we can deduce, the promise is broken whenever I pay \$100. So it's the opposite of before ($\lnot P$). Symbolically: $P \to \lnot P = \lnot P$

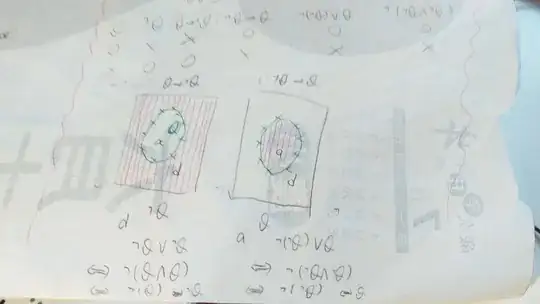
As a venn diagram

A useful rule to keep in mind is that: $P \to Q = \lnot P \lor Q$.

So:

• $P \to \lnot P = \lnot P \lor \lnot P = \lnot P$
• $\lnot P \to P = \lnot \lnot P \lor P = P$

As a venn diagram this view also helps since: $\lnot P$ can be seen as "everything that's not in P".

And $\lor$ can be interpreted as combining the two venn-diagrams.

So your statement: $P \to \lnot P = \lnot P \lor \lnot P$, illustrated here:

Which you can see at the end just equals $\lnot P$.

For your other one: $\lnot P \to P = \lnot \lnot P \lor P = P \lor P$, illustrated here:

Which ends up as just $P$.

(I've written $u$ as the universe in the image out of habit, which you seem to have used $d$ instead, presumably as the domain of discourse which is also correct.)

Validity of $P \to \lnot P$

Usually when we talk about an argument being valid, we have a set of premises: {"Socrates is a man", "All men are mortal"}, and a conclusion "Socrates is mortal".

Symbolically: $(\text{"Socrates is a man"} \land \text{"All men are mortal"}) \to \text{"Socrates is mortal"}$

An equivalent definition of validity is:

An argument is valid if and only if it would be contradictory for the conclusion to be false if all of the premises are true

Here the premises is the set: {"Socrates is a man", "All men are mortal"}, and we ask:

Would it be contradictory for "Socrates is mortal" to be false if "Socrates is a man" and "All men are mortal" are both true?
Yes! Therefore it is valid.

If your asking if $P \to \lnot P$ is valid, we'll take the premises as the set $\{ P \}$, and we ask:

Would it be contradictory for $\lnot P$ to be false if $P$ was true?
No. This it is not contradictory, rather very natural.

So the statement $P \to \lnot P$ invalid.

In propositional logic, these valid arguments are tautologies, basically statements which are always true. As you can see $P \to \lnot P$ is not always true.

Answer 2

$P \Rightarrow Q$ is like a claim.

Conventions vary, but some (many?) authors read $$P \Rightarrow Q$$ as a metalogical assertion that the logical operation (or truth function) $$P \to Q$$ is true (which means that either $P$ is false or $Q$ is true).

($P$ and $Q$ and $P \to Q$ and $P \Rightarrow Q$ are all sentences.)

$P$	$\lnot P$	$P \Rightarrow \lnot P$
True	False	False
False	True	True

Is an implication of the form $P \Rightarrow \lnot P$ valid or not valid?

The third column of the above truth table shows that the sentence $$P \to \lnot P$$ is a contingency, i.e., a sentence that is neither a tautology nor a contradiction. In propositional (though not in first-order) logic, tautology and validity are synonyms; so, the sentence is certainly not a validity.

Based on the above convention (where we read $\Rightarrow$ as asserting that $\to$ is true), the implication $$P \Rightarrow \lnot P$$ is therefore actually asserting that sentence $P$ is false.

But what is its meaning and venn diagram?

Since Venn diagrams deal with sets of objects, I'd rewrite $$P \Rightarrow \lnot P$$ as $$\forall x\;\big(P(x) \Rightarrow \lnot P(x)\big),$$ which is illustrated as a sunny-side-up where the yolk represents $P(x)$ and the entire egg represents $\lnot P(x).$ However, $P(x)$ and $\lnot P(x)$ are disjoint, so have an empty intersection. Therefore, $P(x)$ is actually the empty set, i.e., $P(x)$ is true for no $x,$ i.e., $P$ is false. This conclusion is consistent with that in the previous paragraph.

Summarising: $$P \to \lnot P\quad \equiv\quad \lnot P.$$

Answer 3

Not sure how useful a Venn diagram would be here, but if $P$ is true implies $P$ is false, then $P$ must be false.

Symbolically: $(P\implies \neg P)\implies \neg P$.

Here is the truth table:

Source: https://www.erpelstolz.at/gateway/TruthTable.html

Here is a formal proof by contradiction using a form of natural deduction (screenshot from my proof checker):

Answer 4

I'd approach it via the adjunction $$R\to (S\to W)\ \ \iff\ \ (R\land S)\to W$$

Examples:

"If it's a rainy day, then if I'm also out on the street, then I'm gonna be wet."

"If it's a rainy day and I'm also out on the street, then I'm gonna be wet."

---

Now you can read $\neg P$ as $P\to \bot$ where $\bot$ denotes any false claim. To say $P$ is false is to say that it implies something absurd. With this,

$$P\to \neg P\ \ \iff\ \ P\to (P\to\bot)\ \ \iff\ \ (P\land P)\to \bot\ \ \iff\ \ \neg (P\land P)\iff\ \ \neg P$$

So $P\to \neg P$ is a weird way of saying $P$ is false, just like $\neg (P\land P)$ would be a weird way of saying it.

You could just tell your friend ($\neg P$)

"I would not enjoy having to wake up so early tomorrow."

Where I translate "$P$" to a the waking up task and the negation "$\bullet\to\bot$" to non-enjoyment.

But you could also tell your friend, along the lines of the latter variant ($\neg (P\land P)$)

"I would not enjoy, both having to wake up so early tomorrow and having to wake up so early tomorrow."

but the second is redundant from a classical logic perspective. Indeed so redundant that it would be weird to even say it.

Roughly framing would be along the lines of ($P\to \neg P$)

"If I would have to wake up so early tomorrow, then I would not enjoy it (having to wake up so early tomorrow)."

Indeed the semantics of $P\to (P\to Q)$ is that of $P\to Q$ for the same reason.

Answer 5

P ⇒ ¬P is a contradiction and therefore it's invalid. I mean, if P is true then P is... not true? But we just said P is true. That doesn't work and therefore a truth table can't be constructed.