Star of David theorem proof

Question

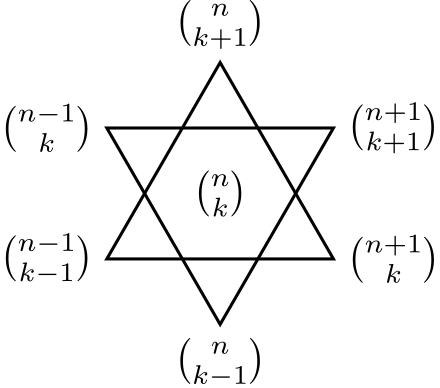
The star of david theorem says:

gcd$\left\{ \binom{n-1}{k-1},\binom{n}{k+1},\binom{n+1}{k} \right\}=$gcd$\left\{ \binom{n-1}{k},\binom{n}{k-1},\binom{n+1}{k+1} \right\}$

I've been looking for a proof of this theorem, but can't find it. Does anyone have a bibliography where I can find the proof?

In EXTENSIONS OF THE HERMITE G.C.D. THEOREMS FOR BINOMIAL COEFFICIENTS it is shown that:

$\frac{n}{(n,k)}$gcd$\left\{\binom{n}{k},\binom{n-1}{k-1}\right\}=\frac{n+1-k}{(n+1,k)}$gcd $\left\{\binom{n}{k},\binom{n}{k-1}\right\}=\binom{n}{k}$

$(n,k)$ denotes the greatest common divisor of $n$ and $k$.

Maybe the theorem is proven from this equality, but I can't see it.

Answer 1

The gcd property is proved in

A. P. Hillman & V. E. Hoggatt, Jr. "A Proof of Gould's Pascal Hexagon Conjecture." Fibonacci Quarterly 10 (1972): 565-68, 598.

available online at https://www.fq.math.ca/10-6.html.