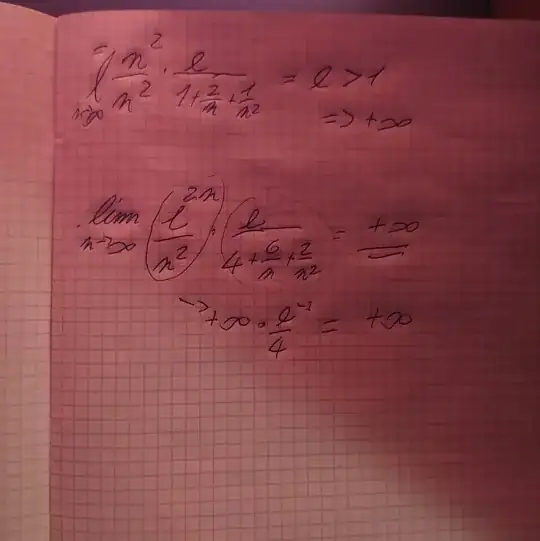2

Evaluate $\lim_{n\to\infty}\frac{e^{n^{2}}}{(2n)!}$.

I used the ratio test to calculate this limit, and I got here:

$\lim_{n\to\infty}\frac{e^{2n}}{n^2}\frac{e}{4+6/n+2/n^2}$.

For the first fraction, I applied the ratio test again and got +inf.

I also attach pictures with a more detailed solution. I would like to ask if the procedure and result are correct.

enter image description here

enter image description here

amWhy
  • 209,954
Aaron7
  • 289
  • 2
    The limit graphically goes to infinity. Also, the writing is hard to see, so please try to use MathJax – Тyma Gaidash Dec 29 '21 at 22:45
  • I have read through your solution, and it seems fine! You might have heard of the phrase "The exponential $x\mapsto e^x$ grows faster than any polynomial in $x$ for $x\to \infty$". This is another manifestation of this fact. – Stardust9922 Dec 29 '21 at 22:55
  • 2
    Your calculations look fine, but you should explain how they answer the question. Specifically, your last step says that a particular limit diverges to $\infty$, but that particular limit is not the limit you were asked to evaluate... – Steve Kass Dec 29 '21 at 22:59
  • You get the same result if you take the natural log of the initial function then take the limit. $\approx x^2-x\ln{x}$ approaches infinity. – TurlocTheRed Dec 29 '21 at 22:59
  • @Stardust9922 I was confused by the factorial, because it generally grows the fastest. – Aaron7 Dec 29 '21 at 23:05
  • Ratio test doesn't make sense, you are taking a limit not computing the convergence of a series right? – Ninad Munshi Dec 29 '21 at 23:07
  • @NinadMunshi Although you're right that the ratio test is used for series and not limits, there is a similar argument you can make where if $\lim_{x \to \infty} f(x)$ is finite, then $\lim_{x \to \infty} \frac{f(x + 1)}{f(x)} = 1.$ Here that limit doesn't go to $1$ so the limit cannot be finite. I'm not sure if the OP knows this but the argument actually does work out – Stephen Donovan Dec 29 '21 at 23:17
  • I would try to use Stirling's approximation, and then take logarithm of the original expression and let $\ n\to\infty,\ $ giving us that the logarithm of the original expression $\ \to\infty\ $ as $\ n\to\infty,\ $and then suggest that this implies the original limit $\ \to\infty\ $ as $\ n\to\infty.\ $ But I'm not sure how sound this method is. – Adam Rubinson Dec 29 '21 at 23:30
  • A hint for doing this by examining factors: $\frac{e^{4^2}}{8!}=\frac{1}{1}\frac{e}{2}\frac{e^2}{3}\frac{e^2}{4}\frac{e^2}{5}\frac{e^2}{6}\frac{e^2}{7}\frac{e^3}{8}\cdot e^2>e^2$. – 2'5 9'2 Dec 30 '21 at 19:21

3 Answers3

3

perhaps it becomes clearer that the limit is infinite, making the series expansion of the exponential

$$ \dfrac{e^{n^2}}{(2n)!} = \dfrac{\sum_{m=0}^{\infty}\dfrac{(n^2)^m}{m!} }{(2n)!} \geq \dfrac{n^{4n}}{ ( (2n)!)^2 }= \left( \dfrac{n^{2n}}{ (2n)! } \right)^2 $$ the last expression on the right is $\geq Cn$ ($C>0$) for large n.

Ilovemath
  • 2,921
  • 1
    "the last expression on the right is $\geq Cn$ ($C>0$) for large n." Why? – Gary Dec 30 '21 at 00:23
  • See https://math.stackexchange.com/questions/61713/whats-the-limit-of-the-sequence-lim-limits-n-to-infty-fracnnn – Ilovemath Dec 30 '21 at 03:50
1

HINT:

Note that we can write $\displaystyle \frac{e^{n^2}}{(2n)!}$ as

$$\frac{e^{n^2}}{(2n)!}=e^{n\left(n-\frac1n\log((2n)!)\right)}$$

Now, show that $\lim_{n\to\infty}\left(n-\frac1n\log((2n)!)\right)>0$ (in fact, the limit is $\infty$).

HINT $2$:

Use the fact that

$$\begin{align} \frac1n\log((2n)!&=2\log(2n)+\frac2{2n}\sum_{k=1}^{2n}\log(k/2n)\\\\ &=2\log(2n)-2 +o(1)\,\,\text{as}\,\,n\to\infty \end{align}$$

Can you proceed now?

Mark Viola
  • 179,405
1

By Stirling's approximation $$\frac{e^{n^{2}}}{(2n)!} \sim \frac{e^{n^2} e^{2n}}{\sqrt{4\pi n} (2n)^{2n}} \sim \frac{1}{\sqrt{4\pi }} \exp \left(n^2 + 2n - 2n \log(2n) - \frac{1}{2}\log(n) \right) \longrightarrow +\infty$$

as $n \rightarrow +\infty$.

TheSilverDoe
  • 29,720