Say we know that $P(k) \implies P(k+3)$. Then if we know $P(1)$ is true, we know $P(4), P(8) \dots$ are also true.
However if we know $P(1)$ is false, does that mean $P(4), P(8) \dots$ are also false?
I'm a little confused on if we can trust an implication which is of the form, false $\implies P(x)$.
Here's a simple example to drive the point home in this specific case: let $P(n)$ be the predicate '$n$ is greater than $2$'. Then if $P(k)$ is true, we have $k+3\gt k\gt 2$, so $P(k+3)$ is true; thus $P(k)\implies P(k+3)$. What's more, $P(1)$ is manifestly false; $1$ is certainly not greater than $2$. But in fact, $P(4)$, $P(7)$, $\ldots$ are all true.
No, in your example, knowing $P(1)$ is false tells us absolutely nothing about the truth value of $P(n)$, $n> 1$.
Even if we know in advance that the entire implication is true, so that it is true that $P(k) \implies P(k+1)$, and we also learn that $P(k)$ is false, then we still cannot conclude anything about the truth or falsity of $P(k + 1)$, even though the implication is true.
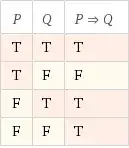
We have defined implication (aka the material conditional), as it is used in logic and in math, such that $$\text{FALSE} \implies P(x)\quad \text{ is always true}.$$
Indeed, by definition: $$P \implies Q \quad \text{is FALSE if and only if}\;\; P \;\;\text{is true}\;\;{\bf and}\;\; Q \;\;\text{is false}.$$
Recall the truth-table for the implication $P\implies Q$ which gives all possible truth-value assignments to P and Q, and the resultant truth value of $P\implies Q$:
No. $P(x)$ can either be false or true, because the only implication statement that is false is True implies False.
No, a false statement implies a true statement. What I mean is that if $A$ is false and $B$ is true, then the statement $A \implies B$ is true. One way to maybe think about this is to note that $A\implies B$ is equivalent to $\neg A \lor B$ that is not $A$ or $B$. But if $A$ is false, then $\neg A$ is true. And if $B$ is true then true or true is true.
Also if $A$ is false and $B$ is false, then the statement $A\implies B$ is true.
So from this you can take that a false statement implies any statement.
I would recommend reading through this question and answers: True or false? $x^2\ne x\implies x\ne 1$
Or take a look at this: http://www.jstor.org/stable/27961699.
