On the pointwise convergence of $\sum_{n\ge 1} \frac{\sin nx}{n}$ to the sawtooth function in $(-\pi,\pi)$

Question

My question stems from Exercise $8$, in Chapter $2$ of Stein and Shakarchi's Fourier Analysis. I have verified that $$\frac{1}{2i} \sum_{n\ne 0} \frac{e^{inx}}{n} = \sum_{n\ge 1} \frac{\sin nx}{n}$$ is the Fourier series of the $2\pi$-periodic saw-tooth function defined by $f(0) = 0$, and $$f(x) = \begin{cases} \frac{-\pi-x}{2} & -\pi < x < 0\\ \frac{\pi - x}{2} & 0 < x < \pi\end{cases}$$

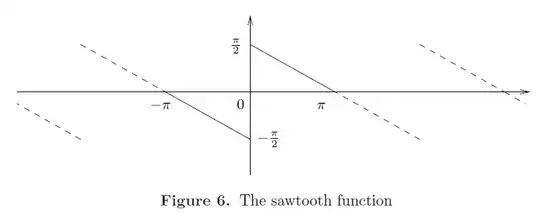
The book says:

Note that this function is not continuous. Show that nevertheless, the series converges for every $x$ (by which we mean, as usual, that the symmetric partial sums of the series converge). In particular, the value of the series at the origin, namely $0$, is the average of the values of $f(x)$ as $x$ approaches the origin from the left and the right.

By Dirichlet's test for convergence, I have shown that $\sum_{n\ge 1} \frac{\sin nx}{n}$ converges for all $x\in (-\pi,\pi) \setminus\{0\}$. At $x = 0$, $\sum_{n\ge 1} \frac{\sin nx}{n}$ clearly converges to $0$. So, $\sum_{n\ge 1} \frac{\sin nx}{n}$ converges for all $x\in (-\pi,\pi)$.

Question: The series $\sum_{n\ge 1} \frac{\sin nx}{n}$ converges to $f$, at $0$. Does it also converge to $f$ at other points in $(-\pi,\pi)$? If yes, how can we show this with elementary methods?

Please note that this is only the second chapter of Stein and Shakarchi's Fourier Analysis, so the machinery we can use is limited. In particular, we can't use Dirichlet conditions, etc.

---

Related questions: Post 1.

---

Edit(s):

1. Integrating the identity suggested by @mathcounterexamples.net from $0$ to $x$, we get $$\sum_{n=1}^N \frac{\sin nx}{n} = -\frac{x}{2} + \frac{\sin Nx}{N} + \int_0^x \sin Nx \cot\frac{x}{2}\, dx$$ I have trouble evaluating the last integral, and don't know how to proceed. For $0 < x < \pi$, we want $$\left|\sum_{n=1}^N \frac{\sin nx}{n} + \frac{x-\pi}{2}\right| =\left|-\frac{\pi}{2} + \frac{\sin Nx}{N} + \int_0^x \sin Nx \cot\frac{x}{2}\, dx\right| \xrightarrow{N\to\infty} 0$$ and for $-\pi < x < 0$, we want $$\left|\sum_{n=1}^N \frac{\sin nx}{n} + \frac{x+\pi}{2}\right| =\left|\frac{\pi}{2} + \frac{\sin Nx}{N} + \int_0^x \sin Nx \cot\frac{x}{2}\, dx\right| \xrightarrow{N\to\infty} 0$$

Answer 1

One way is to start from Lagrange's trigonometric identity

$$\sum_{n=1}^N \cos nx = -\frac{1}{2} + \frac{\sin \left(\frac{(N+1)x}{2}\right)}{\sin \left(\frac{x}{2}\right)}$$ to integrate it and to justify the swap of $\int$ and $\sum$ symbols as $N \to \infty$.

For instance, for $x \in (0, \pi]$ we have

$$\begin{aligned} \sum_{n=1}^N \frac{\sin nx }{n} &= \int_{\pi}^x\sum_{n=1}^N \cos nx \ dx= \frac{\pi - x}{2} + \int_{\pi}^x\frac{\sin \left(\frac{(N+1)x}{2}\right)}{\sin \left(\frac{x}{2}\right)} \ dx\\ &=\frac{\pi - x}{2} + 2\int_{\frac{\pi}{2}}^{\frac{x}{2}}\frac{\sin \left((N+1)u\right)}{\sin u} \ du \end{aligned}$$

Now using the Riemann-Lebesgue Lemma you get

$$\lim\limits_{N \to \infty} \int_{\frac{\pi}{2}}^{\frac{x}{2}}\frac{\sin \left((N+1)u\right)}{\sin u} \ du = 0$$ and therefore the desired result.

Note: see at the bottom of the reference for easy proof of Riemann-Lebesgue lemma using integration by parts which is justified in our case.

Answer 2

Hoping that this could help.

Similar to what you wrote in your own answer, using $$\sum_{n=1}^p \cos(nt)=\csc \left(\frac{t}{2}\right) \sin \left(\frac{p }{2}t\right) \cos \left(\frac{p+1}{2} t\right)$$ the integration gives $$-\frac 12t+\frac{i\,e^{-i p t}}{2 p (p+1)}\Big[(p+1) \, _2F_1\left(1,-p;1-p;e^{i t}\right)+p e^{i (2 p t+t)} \, _2F_1\left(1,p+1;p+2;e^{i t}\right) \Big]$$ which can also write in terms of the incomplete beta function $$-\frac 12t-\frac{1}{2} i \left(B_{e^{i t}}(-p,0)-B_{e^{i t}}(p+1,0)\right)$$ So, the definite integral (from $t=0$ to $t=x$) is $$-\frac 12x-\frac{1}{2} i\Big[\psi(-p)+B_{e^{i x}}(-p,0)-\psi (p+1)-B_{e^{i x}}(p+1,0) \Big]$$

Answer 3

The @mathcounterexamples.net's answer is good, but there is a little bug in the first formula. Actually, $$ \frac 12 + \sum\limits_{k=1}^n \cos kx = \frac{\sin\big(\big(n+\frac 12\big)x\big)}{2\sin \frac x2}, $$ so for $0<x<\pi$ we have $$ \sum\limits_{k=1}^n \frac{\sin kx}k = \frac{\pi - x}2 - \int\limits_{x/2}^{\pi / 2} \frac{\sin(2n+1)u}{\sin u}\,du. $$ The solution could be made more elementary if we avoid using Riemann-Lebesgue Lemma. In order to show that the last integral tends to $0$ as $n\to\infty$, it is enough to integrate by parts: $$ \int\limits_{x/2}^{\pi / 2} \frac{\sin(2n+1)u}{\sin u}\,du = -\frac 1{2n+1} \cdot\left.\frac{\cos(2n+1)u}{\sin u}\right|^{\pi/2}_{x/2} - \frac 1{2n+1}\int\limits_{x/2}^{\pi / 2} \frac{\cos(2n+1)u}{\sin^2 u}\cos u\,du. $$ All functions here are bounded since $0 < \frac1{\sin u} \leq \frac 2x$, so the limit is $0$.