4

Question.

Let $(a_n)$ be a complex sequence defined recursively: $$ a_0 = 0,\quad a_1=1, \quad a_{n}=\frac13(a_{n-1}+a_{n-2}+a_{n-1}a_{n-2})\quad (n>1) $$ What is $\displaystyle\limsup_{n\to\infty}\sqrt[n]{|a_n|}$?

Remarks.

This question is motivated by an unanswered question on the site that I am not able to solve. By the Cauchy-Hadamard theorem, the problem of finding the radius of convergence for the power series $f(z)=\sum_{n=0}^\infty a_nz^n$ reduces to the limit problem above. One can probably find some other way to figure out the radius of convergence, but I would like to focus on Cauchy-Hadamard and thus particularly the limit in the question.

One straightforward attempt is to find a closed-form formula for the sequence so that one may able to apply asymptotic techniques to analyze $|a_n|^{1/n}$. While there are systematic ways to handle the linear recurrence, I don't know how to handle this particular nonlinear case. The usual idea of "linearizing the nonlinear problem" seems not helpful here.

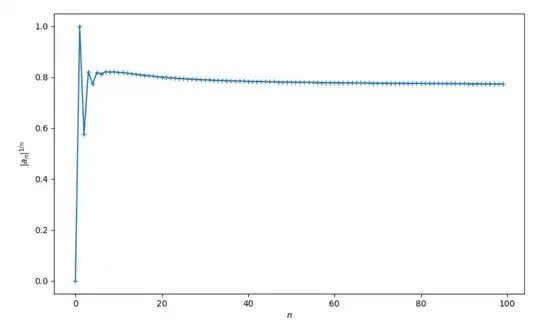
With help of the short Python script, I plotted the sequence $(|a_n|^{1/n})$. The result seems to suggest that the limit is $1$.

enter image description here

  • 1
    one can easily show by induction that $a_n \le \frac{20}{19}(\frac{19}{20})^n$ (enough to check it for $n=1,2,3$ as it6 then follows for $n \ge 4$ by substitution) which shows that $\limsup_{n \to \infty}a_n^{1/n} \le 19/20$ and then @Oliver comment should give the radius as the bigger root of $3x^2-x-1=0$ – Conrad Dec 04 '21 at 18:57
  • @Conrad: Interesting. How do you figure out the magic dominant geometric sequence? Particularly, where are the numbers $20/19$ and $19/20$ from? –  Dec 04 '21 at 19:48
  • If you think a little, you realize that something like $a_n \le Kc^n$ may work as long as $c<1, 3c^2-c-1>0$ and $c$ close enough to $1$ as the product decreases much faster and then since $a_1=1, K=1/c$ is natural and I tried first $9/10$ but that required $n \ge 7$ for the inequality to go by substitution (as it comes down to smallest $n$ for which $3c^2 \ge 1+c+Kc^{n-1}$, so one has to check the first cases...) while the next simple fraction $19/20$ worked from $n \ge 5$ and there the check is easy – Conrad Dec 04 '21 at 20:31
  • It's actually $3c^2 \ge 1+c+Kc^{n+1}$ for $a_m \le Kc^m, m \le n$ to imply $a_{n+1} \le Kc^{n+1}$; so for $c=19/20, K=20/19$ one needs $.7575 \ge .95^n$ so actually I was a bit wrong and one needs $n \ge 6$ but still it works easily... – Conrad Dec 04 '21 at 20:44

2 Answers2

2

Hint:

$$\frac{a_n}{a_{n-1}}=\frac13\Big(1+\frac{a_{n-2}}{a_{n-1}}+a_{n-2}\Big)$$

Show that $a_n\xrightarrow{n\rightarrow\infty}0$ and deduce that $x_n:=\frac{a_n}{a_{n-1}}$ converges to some $x>0$ satisfying $$x=\frac{1}{3}\Big(1+\frac{1}{x}\Big)$$

Recall that $$\liminf_n\frac{|a_{n+1}|}{|a_n|}\leq\liminf_n\sqrt[n]{|a_n|}\leq\limsup_n\sqrt[n]{|a_n|}\leq\limsup_n\frac{|a_{n+1}|}{|a_n|}$$

Another approach, is to consider the discrete dynamical system on $\mathbb{R}^2$ given as \begin{align} \boldsymbol{x}_{n+1}&=G(\boldsymbol{x}_n)\\ \boldsymbol{x}_0 &= \begin{pmatrix} 0\\1\end{pmatrix} \end{align} where $$ G(x,y)=\begin{pmatrix} 0 & 1\\ \frac13 & \frac13 \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix} + \frac13\begin{pmatrix} 0\\ xy \end{pmatrix} $$ The eigenvalues of the linear part of $G$ around the critical point $\boldsymbol{x}^*=[0\;0]^\intercal$ are $\frac{1\pm\sqrt{13}}{6}$.

From this, one can show that with initial conditions closed enough to $\boldsymbol{x}^*$, $\boldsymbol{x}_n$ converges to $\boldsymbol{x^*}$ exponentially fast (the rate of convergence being $\frac{1+\sqrt{13}}{6}$ which is happened to be $\lim_n\frac{a_{n+1}}{a_n}$ where $\boldsymbol{x}_n:=[a_{n-1}\,a_n]^\intercal $.

Mittens
  • 39,145
  • Thanks. If the limit of the sequence $(a_n)$ exists, then it must be zero by the recurence. It is easy to see it is bounded from below. So being (eventually) decreasing would be sufficient. I don't see a natural way to show $a_{n+1}\le a_n$ for sufficiently large $n$. How would you show that the limit exists? –  Dec 04 '21 at 19:58
  • 1
    @ripples: there are several ways to do it. For example, you can follow Conrad's suggestion (use induction) to show that $a_n\xrightarrow{n\rightarrow\infty}0$. Also, (again induction) you can show that $0<a_n<a_4=\frac59$ for all $n>4$ and that $a_n$ is decreasing for $n\geq 5$ and that $a_n<a_4 a_{n-1}$ for all $n\geq 5$. – Mittens Dec 04 '21 at 20:13
  • I got the $a_n\to0$ part. Thanks again. How do you show that $(x_n)$ is convergent? –  Dec 04 '21 at 23:15
  • 1
    Notice that $x_n$ is closed to satisfying the sequence $y_n$ that satisfies $y_{n+1}=\frac13(1+\frac{1}{y_n})$ and that for $n\geq 7$, $x_n<\frac89$. The sequence $y_n$ with $y_{n_0}>1$ can be easily shown to converge. – Mittens Dec 05 '21 at 03:24
  • I don't follow why $y_n$ can be easily shown to converge. Could you elaborate? I also do see that how the convergence of $y_n$ implies that of $x_n$. –  Dec 06 '21 at 15:06
  • $y_n=f(y_{n-1})$ where $f(y)=\frac13\Big(1+\frac1y\Big)$, $y>0$. There is a fixed point $y^$ and at this point $|f'(y^)|<1$. Hence $y^*$ is asymptotically stable (all this follows from the mean value theorem). The second question is more complicated but the idea is that $x_n$ and $y_n$ differ by "very little". – Mittens Dec 06 '21 at 19:16
  • Thanks. I will try to see if I can work out the details. In case this exchange of comments is too long, I have written a related question: https://math.stackexchange.com/q/4324896 –  Dec 06 '21 at 19:17
1

I finally figure out the details to follow Oliver's hint and I would like to write out an answer here.

The two essential steps are proving that the sequences $(a_n)$ and $(\frac{a_n}{a_{n-1}})$ are both convergent. These two steps are nontrivial (!) and they are answered in the following two follow-up posts:

It then follows by straightforward calculations that $$ \lim_{n\to\infty}\frac{a_{n}}{a_{n-1}} = \frac16(1+\sqrt{13}). $$

Consequently, by a well-known theorem (see, e.g., Rudin's Principle of Mathematical Analysis) which compares the ratio and root test: $$ \liminf _{n} \frac{\left|a_{n+1}\right|}{\left|a_{n}\right|} \leq \liminf _{n} \sqrt[n]{\left|a_{n}\right|} \leq \lim _{n} \sup \sqrt[n]{\left|a_{n}\right|} \leq \limsup _{n} \frac{\left|a_{n+1}\right|}{\left|a_{n}\right|} $$ the desired result follows.

Remark.

It is worthing knowing that, in Python, one needs a good algorithm to calculate the $n$-th root for very big $n$. In the original attempt mentioned in the post, the total iteration number was taken too big that the plot is actually not accurate because a**(1/n) was used in the code to find the $n$-th root. However, if one only iterates 100 times, one gets $b_{100}\approx 0.76759187924+\pm 10^{-11}$ which is an approximate value of $\frac{1}{6}(1+\sqrt{13})$.

enter image description here