Let $A=(B\cap C) \cup (D\cap E)$ be a given set. I am looking for a different way to write this. I guess it is somehow possible to "reorder" this by using De Morgan's relations. Unfortunately, I am not successful. Does somebody see how one can write this differently?
Asked
Active
Viewed 279 times
3
-
This is definitely not a duplicate of #402054 as it pertains to four different sets. – Lord_Farin Jun 29 '13 at 11:05
-
I don't see a way to simplify, I think it's basically the simplest way to write down this set. – Henno Brandsma Jun 29 '13 at 11:24
-
1@Henno: I don't see the word "simplify" in this page prior to your comment. – Asaf Karagila Jun 29 '13 at 11:26
-
This is a good question and does not deserve to be closed. – goblin GONE Jun 29 '13 at 11:53
2 Answers
4
You can't use DeMorgan laws here, but you can use the distributivity of $\cap$ over $\cup$ and vice versa. We have:
$$(B\cap C)\cup(D\cap E)=((B\cap C)\cap D)\cup((B\cap C)\cap E)$$
Using associativity of $\cap$ we get:
$$(B\cap C\cap D)\cup(B\cap C\cap E)$$
It's not simpler than the original form, though. Note that you can do the same thing by distributing $D\cap E$ over the other pair, so we get the following: $$(B\cap C)\cup(D\cap E)=(B\cap C\cap D)\cup(B\cap C\cap E)=(B\cap D\cap E)\cup(C\cap D\cap E)$$
Asaf Karagila
- 393,674
3
As pointed out by Asaf Karagila, there is no option to rewrite your expression in a simpler or more elegant way.
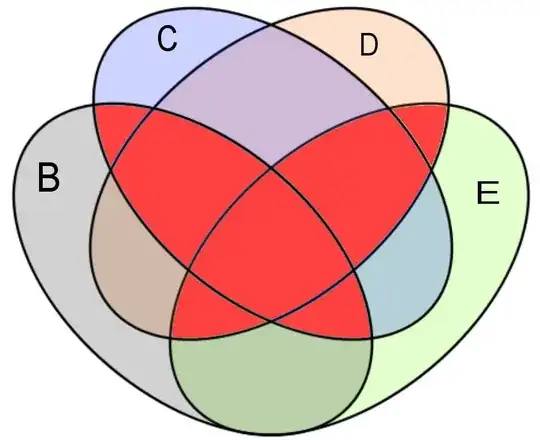
This can be demonstrated graphically:
The following is a Venn diagram for your case:
And here is the Karnaugh-Veitch map:
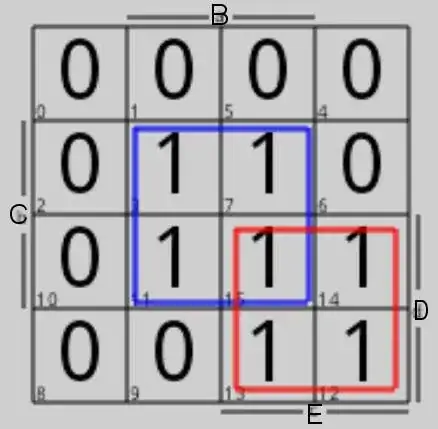
The two intersecting minterm blocks cannot be replaced by fewer or simpler minterm blocks.
Axel Kemper
- 4,943