What goes wrong in my parametric equation for it to produce only a partial rotation of the graph of $f(x)=\cos(x)$?

Question

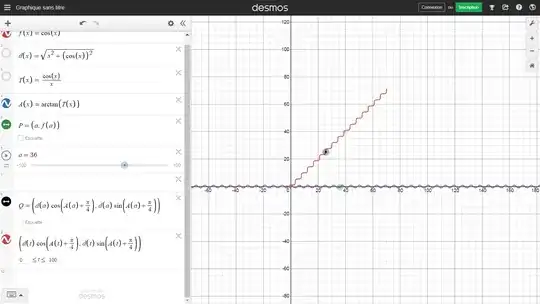
As a pastime, I'm trying to rotate the graph of $f(x)=\cos(x)$ about the point $O=(0,0)$, and I chose, arbitrarily, a rotation of $\pi /4$ radians.

My question is : how comes the parametric equation I came up with only works for the part of the graph that is to the right of $O=(0,0)$?

I reasoned as follow : rotating the graph is tentamount to rotating each point $P=(x, f(x))$ by $\pi/4$ rd. on a circle ( one for each point) centered at $(0,0)$ and of radius $OP = \sqrt {x^2+f(x)^2}$.

So I defined the following auxiliary functions :

(1) Let $OP= d(x)= \sqrt {x^2 + f(x)^2}$

(2) Let $T(x)=$ slope of $OP = \cos(x)/x$

(3) Let $A(x)$= angle of $OP$ with the $X-$axis $= \arctan (T(x))$.

Inasmuch as each point $P$ is supposed to turn on a circle of radius $d(x)$ and of center $O$, trigonometry can be used which gives ( with $P'$ denoting the image of $P$ under the expected $\pi/4$ counterclockwise rotation) :

• $X$ coordinate of $P'$ : $d(x)\cos(A(x)+\pi/4)$

• $Y$ coordinate of $P'$ : $d(x)\sin(A(x)+\pi/4)$.

Hence the parametric equation :

$\bigg<d(t)\cos(A(t)+\pi/4), d(t)\sin(A(t)+\pi/4)\bigg>$

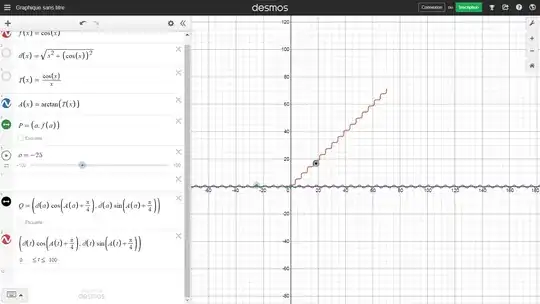
However, this parametric equation produces the desired result only for positive values of $t$ ( or of $x$).

Probably some feature of the $\tan(x)$ function could explain this, but I cannot identify which one it is.

here : a link to my attenpt using Desmos https://www.desmos.com/calculator/mjj6mnr55t

Below, an image for $x\gt 0$

Here , an image of what happens when $x\lt 0$ , point P is in green , its "image " under the parametric function is in dark grey.

Answer 1

By OP's request, a short explanation of the matrix formula: The matrix $$ \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} $$ is the $2 \times 2$ rotation matrix by $\theta$ radians, as can be observed by noting that the first column is the anticlockwise rotation of the unit vector $(1, 0)$ by $\theta$ radians, and the second column is the same transformation of $(0, 1)$. (Draw some triangles with hypotenuse $1$ to convince yourself of this if you haven't played this game before!)

Hence if you take any point/vector $(x, y)$ in the plane and multiply it by this matrix, you get precisely the same point back, only rotated $\theta$ radians anticlockwise.

For our purposes, the points we are interested in are the points $(x, f(x))$ on the graph, so $$ \begin{pmatrix} \cos(\theta) & -\sin(\theta) \\ \sin(\theta) & \cos(\theta) \end{pmatrix} \begin{pmatrix} x \\ f(x) \end{pmatrix} = \begin{pmatrix} x \cos(\theta) - f(x) \sin(\theta) \\ x \sin(\theta) + f(x) \cos(\theta) \end{pmatrix} $$ is exactly the rotation (by $\theta$ radians anticlockwise) of the graph in question.

Specialising at $\theta = \pi/4$ then gives the parametrisation $$ \Bigl( \frac{x - f(x)}{\sqrt{2}}, \frac{x + f(x)}{\sqrt{2}} \Bigr) $$ since $\cos(\pi/4) = \sin(\pi/4) = 1/\sqrt{2}$.