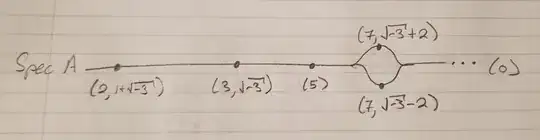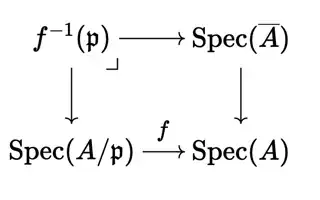I'm a bit confused by the argument that you made in your edit... I would dissuade you from trying to work with "nested" objects like $\mathbb{Z} \left [\sqrt{-3} \right ][x]$ unless absolutely necessary, because (at least for me) they're much trickier to reason about than classical polynomials. It sounds like you have the right general idea, but you might be a bit confused on the details. In particular it does matter what happens to $x^2 + 3$ mod $p$ for various $p$ when it comes to computing prime ideals. It only doesn't matter for this problem because we're interested in how the prime ideals in $A$ compare to those in $\overline{A}$.
To try to clear things up, I'll try to be fairly detailed in how you might attack this problem. Moreover,
since you mention you aren't familiar with tensor products as a means of getting at the fibres, I'll include a more pedestrian approach. I can't help but try and explain why the tensor product "trick" works, though, so you'll have to forgive a quick digression.
With that out of the way, on with the show ^_^.
First, what are the (nonzero) primes in $A$? Well, if we write $A = \frac{\mathbb{Z}[x]}{x^2 + 3}$, then we see the prime ideals in $A$ are exactly the prime ideals in $\mathbb{Z}[x]$ that contain $x^2 + 3$. We know that these look like $(p,f)$ where $f$ is irreducible mod $p$, and so we're looking for ideals $(p,f)$ where $f \mid x^2 + 3$ (mod $p$). Of course, we'll write this polynomial $f$ as $f(\sqrt{-3})$ instead of $f(x)$ (since $x = \sqrt{-3}$ in our ring).
For example, let's compute the primes that lie over $(2) \in \mathbb{Z}$. That is, the primes where $p = 2$.
We want to know that
$$
\frac{A}{\left (2,f \left (\sqrt{-3} \right) \right )}
\cong \frac{\mathbb{Z}[x]}{(x^2+3,2,f)}
\cong \frac{\mathbb{F}_2[x]}{(x^2 + 1, f)}
$$
is a field. Of course, the only way to do this is to choose $f = x+1$, which gives us the prime
$\left ( 2, \sqrt{-3}+1 \right)$.
Doing this for a few other primes, we can draw a quick picture of $\text{Spec}(A)$:
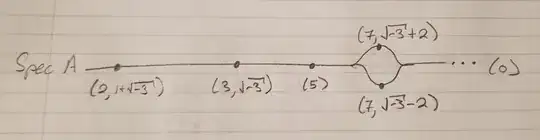
(If it's not clear why this is the spectrum, you should work these out in a way analogous to the example for $p=2$ above!)
Now, let's take a look at $\overline{A} = \frac{\mathbb{Z}[y]}{y^2 - y + 1}$. Again, elements of the spectrum will look like $(p,f)$ where $f$ is irreducible mod $p$, but now we want $f \mid y^2 - y + 1$ (mod $p$).
Again, let's look at the case $p=2$. Then we want
$$
\frac{\mathbb{Z}[y]}{(y^2 - y + 1, 2, f)}
\cong \frac{\mathbb{F}_2[y]}{(y^2 + y + 1, f)}
$$
to be a field. Of course, we know that $y^2 + y + 1$ is $\mathbb{F}_2$-irreducible, so $f = y^2 + y + 1$ is our only choice, and we see our prime ideal is just $(2)$ (notice we don't get $(2,f)$, because we already quotiented by $f$ in the passage from $\mathbb{Z}[y]$ to $\overline{A} = \frac{\mathbb{Z}[y]}{f}$!).

Notice the spectrum for $\overline{A}$ looks superficially similar to the spectrum of $A$ above every prime except $(2)$. We haven't worked out anything to do with the map $\text{Spec}(\overline{A}) \to \text{Spec}(A)$, but now we might have an intuitive plan for what we should look for algebraically!
Inspired by the geometry above, we're led to consider the primes above $(2)$ separately from the other primes. We can get at just the odd primes by localizing at the "function" $2$ (that is, by formally inverting $2$ by adjoining $\frac{1}{2}$).
So, we localize and the inclusion $A \to \overline{A}$ becomes the inclusion
$A \left [ \frac{1}{2} \right ] \to \overline{A} \left [ \frac{1}{2} \right ]$.
Of course, if we expand this out, we see we're looking at the map
$\mathbb{Z} \left [ \sqrt{-3}, \frac{1}{2} \right ] \to \mathbb{Z} \left [ \frac{1 + \sqrt{-3}}{2}, \frac{1}{2} \right ]$ which sends $\sqrt{-3} \mapsto \sqrt{-3} = 2 \frac{1 + \sqrt{-3}}{2} - 1$. This is easily seen to be an isomorphism, with inverse given by the map sending $\frac{1 + \sqrt{-3}}{2} \mapsto \frac{1 + \sqrt{-3}}{2} = \frac{1}{2} \left ( 1 + \sqrt{-3} \right )$.
In particular, since this is an isomorphism, it identifies the primes away from $(2)$.
All that's left is to consider what happens over $(2)$. Now, as has been mentioned a few times now, we could handle this case via fibre products. The idea here is that we can find the fibre over $\mathfrak{p}$ by considering the pullback (you should convince yourself of this):
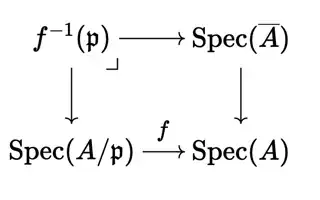
Of course, since the category of affine schemes is dual to the category of rings, we get a pushout of rings:
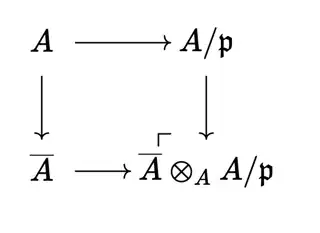
This tells us that $f^{-1}(\mathfrak{p})$ should be
$\text{Spec} \left (\overline{A} \otimes_A A/\mathfrak{p} \right )$,
which is exactly what the comments and the other answer suggest.
It seems like you're looking for an approach that avoids this machinery, though, so let's see another way to do this.
The fibre over $\left ( 2, 1 + \sqrt{-3} \right )$ in $\text{Spec}(A)$ will be exactly the primes in $\text{Spec}(\overline{A})$ which pull back to $\left ( 2, 1 + \sqrt{-3} \right )$ under the natural embedding $A \hookrightarrow \overline{A}$. Of course, there's only one prime that does the job: $(2)$.
But notice
$$
\mathbb{F}_2
\cong \frac{A}{\left ( 2, 1 + \sqrt{-3} \right )}
\hookrightarrow
\frac{\overline{A}}{(2)}
\cong \mathbb{F}_4
$$
is not an isomorphism!
So taking spectra, we find the fibre is $\text{Spec}(\mathbb{F}_4) \to \text{Spec}(\mathbb{F}_2)$, which is a bijection, but not an isomorphism.
At the end of the day, we see every fibre is a singleton, and we get an isomorphism of over every prime except $(2)$.
I hope this helps ^_^