I'm struggling a lot figuring out how to sketch the following $$|x-y|+|x+y|=\sqrt5$$
This is what I know
for$|x-y|$
- $x-y \geq 0$ then $y \leq x$ so $|x-y|= x-y$
- $x-y < 0$ then $y >x$ so $|x-y|= -(x-y)$
for$|x+y|$
- $x+y \geq 0$ then $y \geq -x$ so $|x+y|= x+y$
- $x+y < 0$ then $y <-x$ so $|x+y|= -(x+y)$
but even after knowing this, I still don't know how to sketch it.
The result should look something like this:
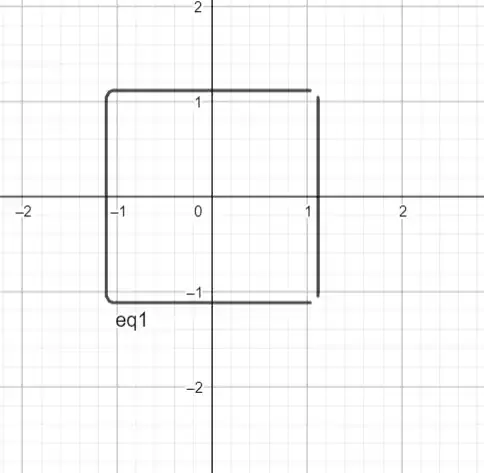
If you could help me it would be very much appreciated.