I'm really doing my best but completely failing to understand the epsilon-delta definition of a limit. I vaguely understand it like this: Given a bound on the difference between the input and desired input, there also exists a bound on the difference between the value of our function and the value of the function at the limit. However, my I have no understanding of where this formal definition came from and what it means at a deeper level, so I feel like it's just been arbitrarily thrown at me by my textbook. Can someone elaborate on its meaning and what this relationship between $$ and $$ signifies? I would appreciate as simple of an explanation as possible.
-
It is not directly answering the question but this little discussion https://math.stackexchange.com/q/3435671/399263 can be a good complement in trying to understand some subtleties about limits. – zwim Nov 18 '21 at 20:53
-
I can provide you with an excellent resource. Which addresses exactly what you are looking for. Link: https://youtu.be/Prwx4vr2l2M – user264745 Nov 18 '21 at 20:55
-
As a further reading, you can use Introduction to metric and topological space by Wilson Sutherland. Second edition, page no. 25. – user264745 Nov 18 '21 at 21:00
-
You can think about $\varepsilon-\delta$ as control; I want to control my function and push its outputs together, not merely close together but as close as I wish, usually stated as "arbitrarily close". If I can't have this control, then I can always stand my ground and say: "No, that is not the limit, we cannot get so close". If we do have this control, then no matter how defiant I am, if I challenge someone to find a value within, say $0.000000001$, then someone can beat me and say "Yes! Such a $\delta$ does exist". Then we have a limit, because I always lose :) – FShrike Nov 18 '21 at 21:29
-
Sorry ! this is the correct link to another question about $\epsilon-\delta$ definition. https://math.stackexchange.com/questions/1489702/how-to-make-sense-out-of-the-epsilon-delta-definition-of-a-limit/1489710#1489710 – Emilio Novati Nov 18 '21 at 21:59
2 Answers
Other answers have talked about the epsilon-delta definition as a game. Maybe it would be helpful to play a couple of rounds of that game to solidify what we are talking about.
Let's play the game with the function $f(x) = x^2 - 2x + 1$. We (team $\delta$) think that the limit of $f(x)$ as $x$ tends to $3$ is $4$. The good news is that we are correct. But our evil opponents (team $\epsilon$) are trying to trip us up by throwing strange values of $\epsilon$ at us.
Maybe their opening gambit is to say: "What about $\epsilon = 10$?". To win the round, we must provide an interval of the form $[3 - \delta, 3 + \delta]$ such that if $x$ is in that interval then $f(x)$ is in the interval $[4 - \epsilon, 4 + \epsilon] = [4 - 10, 4 + 10] = [-6, 14]$.
It is easy for us to repel this first attack. We say: "$\delta = 1$". And sure enough, on the interval $[2, 4]$ the function $f(x)$ takes values in $[1, 9]$. Therefore, the weaker statement that it takes values in $[-6, 14]$ is true and we win that round.
Our opponents get smarter. "Well, what about $\epsilon = 1$?", they ask. Our "$\delta = 1$" response isn't going to cut it this time because we need to find a interval for $x$ where the corresponding $f(x)$ interval is $[4 - 1, 4 + 1] = [3, 5]$. We think a little (but not too much) and suggest "$\delta = 0.1$" because that seems safe. It implies an interval of $[2.9, 3.1]$ for $x$ and $[3.61, 4.41]$ for $f(x)$. So this works fine and we win again.
Now our opponents are angry. "Fine, what about $\epsilon = 0.0000001$?" they smugly demand. We are now getting scared and also a little bored. These guys are going to keep throwing out smaller and smaller values for $\epsilon$ and we are going to need to come up with smaller and smaller values for $\delta$. Can we do it?
That is the general question for delta-epsilon limits. Can we always win the game? If we can, then the limit exists.
The specific details as to how we do this for our $f(x)$ aren't particularly interesting but we might approach it by:
- Noting that $|f(x) - 4| < \epsilon \iff -\epsilon < f(x) - 4 < \epsilon$
- Noting that near $x = 3$, say in the interval $[2, 4]$, $f(x)$ is increasing. That is if $\delta < 1$ then for all $x$ in $[3 - \delta, 3 + \delta]$ we have $f(3 - \delta) < f(x)$ and $f(x) < f(3 + \delta)$
- Finding $\delta$ such that $-\epsilon < f(3 - \delta) - 4$ and $f(3 + \delta) - 4 < \epsilon$ (probably by converting the $<$ signs to $=$, solving the resulting quadratic equations in $\delta$ and maybe nudging $\delta$ a little to ensure that the $<$ holds rather than just $\le$)
Again the specifics for other functions might be very different (and you'll probably go on to prove some theorems to make them easier) but what is important is whether you can produce a winning $\delta$ for any $\epsilon$ thrown at you.
Some final notes:
- In the game our opponents value of epsilon and our responding value of delta must always be strictly greater than zero. Saying "$\epsilon = 0$" or "$\delta = 0$" isn't an allowed move in the game
- Our opponents aren't going to win by throwing larger values of $\epsilon$ at us because we can just repeat our previous $\delta$ and win that round
- We can't just pick a small value of $\delta$ at the start and walk away because our opponent could pull a similar trick to the one we used and produce an $\epsilon$ that breaks our $\delta$. We need to know their $\epsilon$ before producing our $\delta$.
- There is a nice Brilliant article that explains this game approach too
- 528
- 2
- 9
$\lim_{x \rightarrow y}{f(x)} = c $ if and only if for every $ \epsilon > 0 $, there is a $ \delta > 0 $ such that $ 0 < |x - y| < \delta$ implies $ | f(x) - c | < \epsilon $ for all $x$
Lets see what it means.
It's easiest to read $ 0 < |x - y| < \delta $ as "the distance between $x$ and $y$ is between $0$ and $\delta$".
If we use this interpretation, the definition becomes: $\lim_{x \rightarrow y}{f(x)} = c$ if and only if for every $ \epsilon > 0 $, there is a $\delta > 0$ such that if the distance between $x$ and $y$ is between $0$ and $\delta$, the distance between $f(x)$ and $c$ is less than $\epsilon$.
This basically means that $f(x)$ gets arbitrarily close to $c$ without necessarily becoming $c$.
Suppose $f(x)$ does not get arbitrarily close to $c$, i.e., there is some constant $d$ such that $f(x)$ will stay away from $c$ with at least distance $d$. Then we can show the limit definition does not hold: take $\epsilon = d$. Now there doesn't exist a $\delta$ such that $0 < |x - y| < \delta \rightarrow |f(x) - c| < \epsilon $ (because we just assumed that $f(x)$ would never get closer to $c$ than distance $d$, and remember that this happening is equivalent to $|f(x) - c| < \epsilon = d$).
What may be helpful too is a (trivial) proof using the limit definition. Usually in these proofs, you take an $\epsilon$, and return a $\delta$ for which you have proved that $ 0 < |x - y| < \delta \rightarrow | f(x) - c | < \epsilon $ (when dealing with continuous functions you usually just use $|x - y| < \delta$ in your proof). I prove that $\lim_{x \rightarrow y} x = y$ (or, equivalently $f(x) = x$ and $c = y$ in the original formulation).
Take $\delta = \epsilon$. Then $ |x - y| < \delta \rightarrow | f(x) - y | = | x - y | < \delta = \epsilon $. So the condition that there exists some $\delta$ for which $ |x - y| < \delta \rightarrow | f(x) - c | < \epsilon $ holds is true, as I've just shown. More advanced proof usually use a similar logic, but the expression for $\delta$ and working out the $| f(x) - c | < \epsilon$ can become quite hard. This is why other theorems are often used (for continuous functions, $ \lim_{x \rightarrow y} f(x) = f(y) $, and compositions, products, sums of continuous functions are again continuous, which can help you out very often).
Also, the definition requires that something must hold for every $\epsilon$. Sometimes, teachers explain this as a game: you can choose $\epsilon$ freely, and you can give a procedure to show that something (there exists a $\delta$ such that...) will hold, then we can say $\lim_{x \rightarrow y} f(x) = c$. So, if you win this game by giving such a procedure, you basically got the recipe for a proof!
If you cannot win, it suffices to give a single $\epsilon$ such that $f(x)$ will never get closer to $c$ then distance $\epsilon$.
The wikipedia page on the ($\epsilon$, $\delta$)-definition is pretty good. Also, the picture from there may be helpful when you try to visualize $\delta$ and $\epsilon$ as distances.
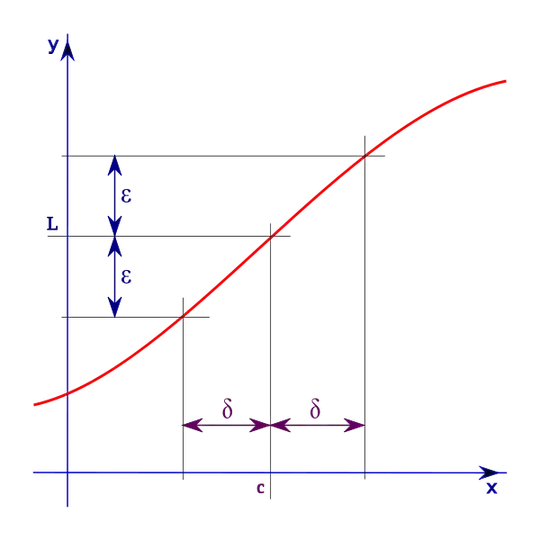
- 26,114
-
2I would tweak your explanation a bit to explain that to "break" a limit, it's not necessary that the function never approach the proposed limit. It's enough if, no matter how close you get, the function sometimes gets "far away" from the proposed limit. Think $\sin \frac 1x$ as $x \to 0$. – Robert Shore Nov 18 '21 at 21:26
-
Thank you, I think my issue was with understanding the significance of delta and epsilon as indicators that the function approaches the same limit over any bounds. – Ethan Dandelion Nov 18 '21 at 21:28
-
1