1

Disclaimer: I am not a mathematician. But I am trying to understand this concept.

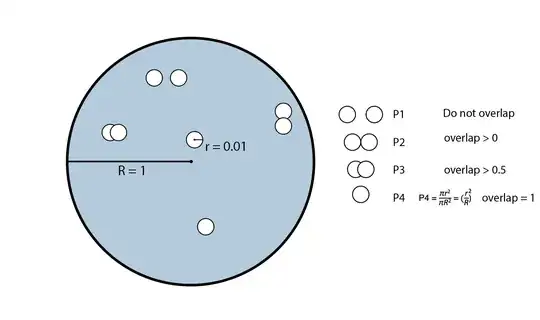
Having a blue circle of area πR2, and a smaller white circle of area πr2, what is the probability that a second, random, and independent, white circle of the same area, will:

1 ) P1 = Miss the first white circle entirely. 2 ) P2 = Intersect with the first white circle > 0 3 ) P3 = Intersect with the first white circle > 0.5 4 ) P4 = Intersect the first white circle entirely.

I calculated P4 simply by getting the fraction of the blue area that is taken by the first white circle. I suspect I would have to square this value since that would mean the chance of this area to be intersected?

Let me know your thoughts,

Thank you for the help =)

enter image description here

Tiago Bruno
  • 165

1 Answers1

1

I think this might work. Instead of considering the smaller circle as a whole, only consider the central point. Then it's like throwing a point on a big circle of radius R-r. For P1, the point must be outside a circle of radius $2r$ centred on the same point as the first small circle, hence $P1=1-\frac{4r^2}{(R-r)^2}$, $P2=\frac{4r^2}{(R-r)^2}$. You can work out P3 yourself. As I mentioned in the comment, $P4=0$.

Tychus Findlay
  • 315
  • Thanks. I like your solution. Based on this, P3 would be 22/(−)2, since the central point would be outside of a circle of radius r. ? – Tiago Bruno Nov 18 '21 at 03:22
  • 1
    No. You need to work out at what distance $k$ between the central points of the first and second small circles, will the overlap be exacted 0.5. I don't know what $k$ is, this thread might help https://math.stackexchange.com/questions/402858/area-of-intersection-between-two-circles. Once you figure out $k$, $P3=\frac{k^2}{(R-r)^2}$ – Tychus Findlay Nov 18 '21 at 03:32
  • Makes sense.. Thanks! – Tiago Bruno Nov 18 '21 at 03:36