How to show geometrically the CDF of the stick problem (with three pieces)?

Question

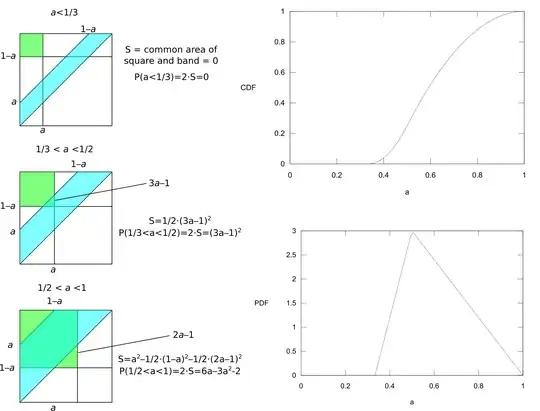
I have come across this classic probability problem and I cannot wrap my head around how this CDF was constructed geometrically.

Can anyone show how we can find the area of P using unit square please?

The original problem is described here, however there are no details provided for this step: Average length of the longest segment.

And here: Stick of unit length is broken into three random pieces, what is the expected length of the longest piece? This part : " A bit of geometry will give you the result " @Canardini

score 1 · Accepted Answer · answered Nov 11 '21 at 16:00

1

$$<a>=\int_{1/3}^{1/2} (18a-6)a\, da+\int_{1/2}^{1} (6-6a)a\, da=$$ $$=(6a^3-3a^2)|_{1/3}^{1/2}+(3a^2-2a^3)|_{1/2}^{1}=$$ $$=(6/8-3/4)-(6/27-3/9)+(3-2)-(3/4-2/8)=11/18$$

answered Nov 11 '21 at 16:00

Ivan Kaznacheyeu

4,188

$P(1/3<a<1/2)$ is not probability of $1/3<a<1/2$ is probability of longest segment to be less than $a$ at certain $a$ in this interval. – Ivan Kaznacheyeu Nov 11 '21 at 16:03
Thank you so much for this reponse. I now can see it! – Karina Nov 11 '21 at 16:11

How to show geometrically the CDF of the stick problem (with three pieces)?

1 Answers1