The 13-node Paley graph has vertices 1 to 13 that are connected by an edge when their difference is one of the values
$(1,3,4,9,10,12)$
Can this graph be put into 3D space so that all edges have length 1, making it a unit distance graph? The graph has chromatic number 5, so this would be a nice object for the 3D Hadwiger–Nelson problem.
No such embedding exists. The proof below is not fully rigorous, but should be convincing enough.
Number the vertices like this:
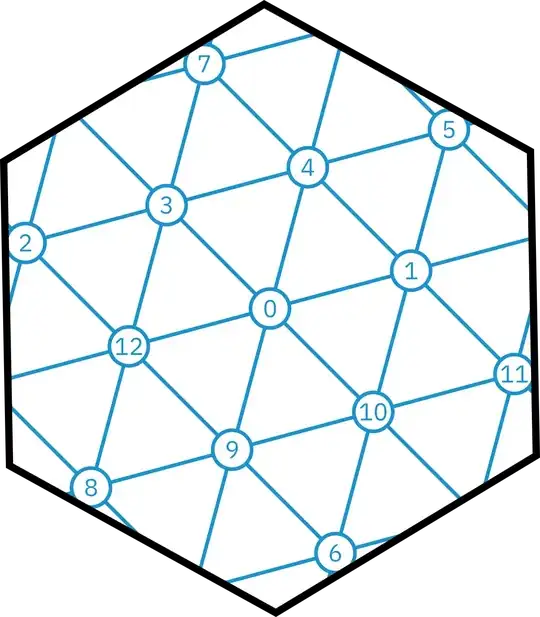
As in this answer I am going to explicitly construct the graph's vertices starting from a few parameters. The following parameters suffice in this case:
By symmetry we can reduce the eight possibilities for the second set of parameters to four: $+++,++-,+--,---$. Without loss of generality we can also fix $0=(0,0,0)$, $1=(1,0,0)$, point $3$ in the $xy$-plane and point $9$ with positive $z$-coordinate – the parameters above then fix points $4,12,10$.
The remaining six points are uniquely determined. To see this, note that $0$ and $2$ are both adjacent to $1,3,12$; with all distances identical and the requirement that vertices not coincide it is easy to deduce that point $2$ must be the reflection of point $0$ in the $1,3,12$ plane. A similar argument applies by rotating the diagram above for the other five "outer" points.
To actually show the non-existence of a 3D unit-distance embedding for Paley-13 we sample over all possible combinations of parameters. For each sample we compute the sum of absolute deviations from $1$ of the nine remaining edges: $$\{(2, 11), (8, 5), (6, 7), (2, 6), (8, 11), (6, 5), (11, 7), (5, 2), (7, 8)\}$$ If Paley-13 had a unit-distance embedding we would expect some samples to have a deviation sum close to zero, but sampling the continuous parameters using a dense lattice yields the following minimal sums for each sign pattern: $$+++:1.2676384880260365\\ ++-:1.6056266375770387\\ +--:1.2143797215919396\\ ---:1.5513409497822102$$ All are far from zero, so we conclude that the Paley graph of order $13$ has no 3D unit-distance embedding.
This is the program I used to derive the minimal deviation sums above.
#!/usr/bin/env python3
import numpy as np
L = 2*np.pi/3
eps = 1e-6
res = 200
coord = np.linspace(eps, L-eps, res+1)
A, B, C = np.meshgrid(coord, coord, coord, indexing="ij")
def tripod(p, q):
# Construct the point at distance 1 from 0, p and q
# such that from its perspective the vertices 0-p-q
# run counterclockwise. Assume |p| = |q| = 1.
diff = q-p
d = (diffdiff).sum(axis=-1)[...,np.newaxis]
k = diff / np.linalg.norm(diff, axis=-1)[...,np.newaxis]
v = -(p+q) / 2
kxv = np.cross(k, v)
kdv = (kv).sum(axis=-1)[...,np.newaxis]
return 2 * (np.sqrt(3-d)kxv + kdvk - v) / (4-d)
def reflect(p, q, r):
# Construct the reflection of the origin in the plane
# defined by p, q, r.
n = np.cross(q-p, r-p)
proj = (np).sum(axis=-1) / (nn).sum(axis=-1)
return 2 * proj[...,np.newaxis] * n
def paleymin(signs):
K0 = np.zeros_like(A)
K1 = np.ones_like(A)
p0 = np.stack([K0, K0, K0], axis=-1)
p1 = np.stack([K1, K0, K0], axis=-1)
p3 = np.stack([np.cos(C), np.sin(C), K0], axis=-1)
dh = (np.cos(A) - np.cos(B)np.cos(C)) / (np.sin(B)np.sin(C))
np.clip(dh, -1, 1, dh)
p9 = np.stack([np.cos(B), dhnp.sin(B), np.sqrt(1-dh2)np.sin(B)], axis=-1)
p4 = tripod(p1, p3) if signs < 1 else tripod(p3, p1)
p12 = tripod(p3, p9) if signs < 2 else tripod(p9, p3)
p10 = tripod(p9, p1) if signs < 3 else tripod(p1, p9)
p2 = reflect(p1, p3, p12)
p8 = reflect(p4, p12, p9)
p6 = reflect(p3, p9, p10)
p11 = reflect(p12, p10, p1)
p5 = reflect(p9, p1, p4)
p7 = reflect(p10, p4, p3)
pts = [p0, p1, p2, p3, p4, p5, p6, p7, p8, p9, p10, p11, p12]
test_edges = ((2, 11), (8, 5), (6, 7), (2, 6), (8, 11), (6, 5), (11, 7), (5, 2), (7, 8))
distances = sum(abs(np.linalg.norm(pts[i]-pts[j], axis=-1) - 1) for (i,j) in test_edges)
return distances.min()
for s in range(4):
print(s, paleymin(s))
