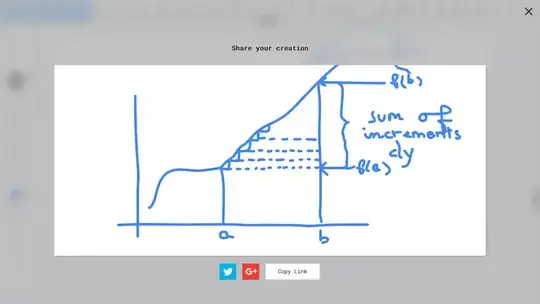
The following setup provides, I believe, an intuitive understanding of the Fundamental Theorem Of Calculus:
(1) $f(x)=y$ is a function defined on the interval going from $x=a$ to $x=b$ and positive on this interval.
(2) at the infinitesimal level , for a small increment of $x$ , $dx$ , every increment of the function $\Delta y $ is $dy= f'(x)dx$ ( because $f'(x)=dy/dx$).
(3) for each value of $x$ in the interval considered, there is an infinitely small triangle, located at $(x, f(x))$, with base $dx$ and height $dy$.
(4) the sum of these heights, projected horizontally on the line passing through $(b, 0)$ and $(b, f(b))$ amounts to the vertival segment having $(b, f(a))$ and $(b, f(b))$ as endpoints, that is, amounts to the height of function $f$ at $x=b$ minus its height at $x=a$, meaning that
$ \int_a^b dy = \int_a^b f'(x)dx = f(b)-f(a)$.
(5) This results says that the sum of the differentals of a function on an interval is equal to the increment of this function. If we call $F(x)=y $ the original function, $f$ its derivative , and denote by $f(x)dx$ its differential, we get the $FTC$ in its ordinary aspect ( Evaluation Theorem version ) :
$ \int_a^b dy = \int_a^b f(x)dx = F(b)-F(a)$
What seems interesting in this interpretation of the $FTC$ is that no use is made of the idea of the " area below the curve".
My questions :
(1) is it correct that the integral can de interpreted as a sum of differentials?
(2) is there a way to prove the $FTC$ in its " differential " version , that is, to prove that the sum of the differentials from $a$ to $b$ is equal to the final height of the function ( at $b$ )minus the original height of the function ( at $a$) ?