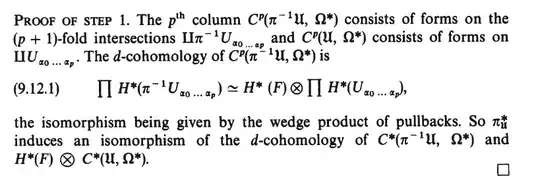I'm reading Bott and Tu's Differential forms in algebraic topology and I'm stuck on their proof of the Kunneth's formula prop 9.12 for when one manifold has finite dimensional de Rham cohomologies.
Basically, if $M,F$ are two smooth manifolds, $F$ has finite dimensional cohomologies in all degree, then $H^n_{dR}(M\times F)=\oplus_{p=0}^n H^p_{dR}F\otimes H^{n-p}_{dR}M$.
I have a question about step 1 of the proof. In particular, why is equation 9.12.1 correct? If we have infinitely many factors in the direct product, then $H^\ast(\pi^{-1}U_{\alpha_0,...,\alpha_p})=H^\ast(F)$ by homotopy equivalence, so we want $\prod H^\ast(F)\cong H^\ast(F)\otimes\prod\mathbb{R}$ which is not true if there are infinitely many factors.