Find $du$ and $dv$ if $u+v=x+y$ and $\frac{\sin(u)}{\sin(v)}=\frac{x}{y}$.
How to solve this?
Found almost an answer: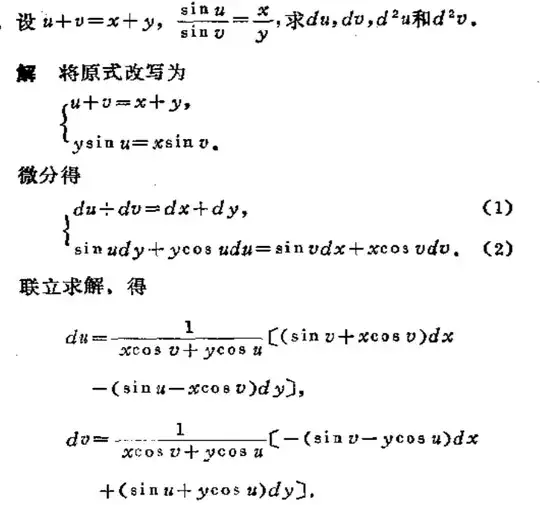
But how do we get $du=...$ from the second?
- 115
-
It's just solving linear simultaneous equations for $du,,dv$. – J.G. Nov 03 '21 at 17:55
-
Ok, I understood how I get the second system from the first, but how do I get du and dv? – sln Nov 05 '21 at 18:38
-
That's the step my last comment discussed. You have equations of the form $Adu+Bdv=E,,Cdu+Ddv=F$ with $AD\ne BC$. – J.G. Nov 05 '21 at 19:14
3 Answers
To expand on my comments, (2) rearranges to $-y\cos u\mathrm{d}u+x\cos v\mathrm{d}v=-\sin v\mathrm{d}x+\sin u\mathrm{d}y$. Then the numbered equations can be restated as$$\left(\begin{array}{cc} 1 & 1\\ -y\cos u & x\cos v \end{array}\right)\left(\begin{array}{c} \mathrm{d}u\\ \mathrm{d}v \end{array}\right)=\left(\begin{array}{cc} 1 & 1\\ -\sin v & \sin u \end{array}\right)\left(\begin{array}{c} \mathrm{d}x\\ \mathrm{d}y \end{array}\right).$$Hence$$\left(\begin{array}{c} \mathrm{d}u\\ \mathrm{d}v \end{array}\right)=\frac{1}{x\cos v+y\cos u}\left(\begin{array}{cc} x\cos v & -1\\ y\cos u & 1 \end{array}\right)\left(\begin{array}{cc} 1 & 1\\ -\sin v & \sin u \end{array}\right)\left(\begin{array}{c} \mathrm{d}x\\ \mathrm{d}y \end{array}\right),$$which is your final pair of equations.
- 115,835
-
Ok, I understood, my other question https://math.stackexchange.com/questions/4283371/understanding-partial-derivatives-computation-issued-from-an-implicit-change-of helped me too. But how to get du=... and dv=... from your last equation? – sln Nov 05 '21 at 19:57
-
-
@whatgenius (1) Just do the matrix multiplications. (Let me know if you'd like me to edit the answer to not use matrices.) (2) An equation such as $\mathrm{d}u=\frac{\partial u}{\partial x}\mathrm{d}x+\frac{\partial u}{\partial y}\mathrm{d}y$ is shorthand for the fact that, if we trace out a path parameterized by a variable $t$, $\frac{\mathrm{d}u}{\mathrm{d}t}=\frac{\partial u}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial u}{\partial y}\frac{\partial y}{\partial t}$; that's all we really mean when we talk about things like $\mathrm{d}u$. (We don't use $\partial u$ in the same way.) – J.G. Nov 05 '21 at 20:22
-
(1) It would be great if you add the variant without matrices. (2) Where is variable $v$? – sln Nov 06 '21 at 06:34
-
If by variant without matrices you mean these multiplied matrices then no need – sln Nov 06 '21 at 06:43
You know they treated $du, dv$ as variables and solved the Linear equation
- So, Is it OK to treat differentials as variables?: YES! The rest you can do either by using Cramer's Rule or else as follow: $$u + v = x + y \implies du + dv = dx + dy $$ $$\color{red}{du} = dx + dy - dv \text{ & } \color{blue}{dv} = dx + dy - du$$
$$y\sin u - x\sin v =0 \implies dyS_u + yC_u\color{red}{du} - dxS_v -xC_v\color{blue}{dv} = 0 $$ $$dyS_u + yC_u\color{red}{du} - dxS_v -xC_v\color{blue}{(dx + dy - du)} = 0 $$ $$\color{red}{du}(yC_u+xC_v) = \left(dx(S_v+xC_y) -dy(S_u-xC_v)\right)$$ $$\implies du = \frac{\left[dx(\sin v+ x\cos y) - (\sin u - x\cos v)dy\right]}{(x\cos v+y\cos u)}$$
-
1In the last and the last but one it is $cos v$ instead of $cos y$ and $C_y$ -> $C_v$ – sln Nov 06 '21 at 07:58
Let $\;u=u(x,y),\;v=v(x,y),\;$ where $\;x\;$ and $\;y\;$ are independent variables.
Then \begin{cases} u_x+v_x=1\\ y\cos u\, u_x=\sin v+x\cos v\, v_x\\ u_y+v_y=1\\ \sin u +y\cos u\,u_y =x\cos v\, v_y, \end{cases} \begin{cases} v_x=1-u_x,\;(y\cos u+x\cos v)\,u_x=\sin v+x\cos v\\ u_x=1-v_x,\;(y\cos u+x\cos v)\,v_x=-\sin v+y\cos u\\ v_y=1-u_y,\;(y\cos u+x\cos v)\,u_y=-\sin u+x\cos v\\ u_y=1-v_y,\;(y\cos u+x\cos v)\,v_y=\sin u+y\cos u. \end{cases}
Finally, $$\text du=u_x\,\text dx +u_y\,\text dy = \dfrac{\sin v+x\cos v}{y\cos u+x\cos v}\,\text dx +\dfrac{-\sin u+x\cos v}{y\cos u+x\cos v}\,\text dy,$$ $$\text dv=v_x\,\text dx +v_y\,\text dy = \dfrac{-\sin v+y\cos u}{y\cos u+x\cos v}\,\text dx +\dfrac{\sin u+y\cos u}{y\cos u+x\cos v}\,\text dy.$$
- 28,026